Untersuchungen von Funktionen und ihren Graphen: Kurvendiskussion der ganzrationalen Funktion
Frage: Für was steht R1 bzw R2 in der folgenden Lösung?
Lösung:
\( D(f)=[-3 ; 6] \)
für \( x \rightarrow x: f(x) \rightarrow \infty \)
für \( x \rightarrow-\infty: f(x) \rightarrow-\infty \)
punktsymmetrisch zum Ursprung \( S_{Y}(0 \mid 0) \)
\( S_{x_{1,2}}(\pm 2 \sqrt{3} / 0)=(\sim \pm 3,46 / 0), \quad S_{x,}(0 \mid 0) \)
\( H(-2 \mid 4) \quad T(2 \mid-4) \)
\( R_{1}\left(-3 /_{4}^{9}\right) \quad R_{2}(6 \mid 36) \)
\( \|(0 \mid 0) \)
\( W(f)=[-4 ; 36] \)
\( f^{\prime}(x)=\frac{3}{4} x^{2}-4 \)
\( f^{\prime \prime}(x)=\frac{3}{2} x \)
\( f^{\prime \prime}(x)=\frac{3}{2} \)
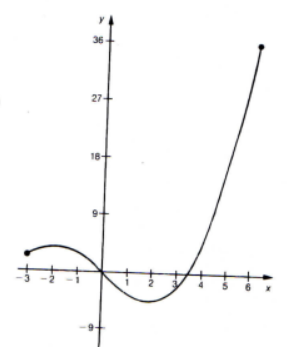
Falls ihr das nicht sofort erkennen könnt, dann rechnet bitte mit folgender Stammfunktion f(x) = 1/4x^3 - 3x.
(Nicht wundern, F'(x) ist in der Lösung nicht korrekt.)