Berechnung der Extrempunkte. Schreibweise und "wo setzte ich was ein"?

Question

Bei einer Funktion 3. Grades ist das alles kein Problem.Bei einer Funktion 4. Grades ist das ein wenig komplizierter für mich da ich zusätzlich eine Polynomdivision mit der 1. Ableitung machen muss und dadurch verwirrt bin.

Folgende Funktion: f(x)= -1/6x⁴+x²-4/3x+1/2

Für die Berechnung der Extrempunkte benötige ich f'(x) also: f'(x)= -2/3x^3+2x-4/3

Für die P/q formel (anders als für die "abc-Formel") muss die Funktion 3. Grades in eine Funktion 2. Grades umgewandelt werden. Also führe ich eine Polynomdivision durch:

1. Frage : Wie schreibe ich nun das Ergebnis der Polynomdivission für den weiteren Schritt auf. (richtige Schreibweise ist gefragt)

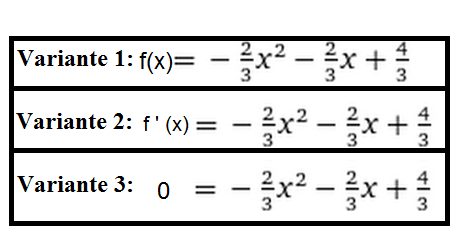
Ich tendiere zu der Variante 3. Da ich für die Nullstellen f'(x) nullsetzen muss. Aber es handelt sich bei dem Ergebnis der Polynomdivission doch überhaupt nicht um die 1. Ableitung ?

Jedenfalls eliminiere ich im weiteren Verlauf den Koeffizienten vor dem x^2 um p Bzw. q heraus zubekommen und setzte diese in die p/q Formel ein.

Ich erhalte x1= 1 und x2 = -2

2. Frage : Jetzt muss Ich herausfinden ob es sich (was ist es ?) um einen HP oder einen TP handelt. In welche Funktion setzte ich dafür x1 / x2 ein ? In f '' (x) oder in das Ergebnis der Polynomdivission. ? Oder ist es das selbe?

Abschließend x1 / x2 in die Stammfunktion -> um den eigentlichen HP / TP zu ermitteln.

Ich Hoffe ich habe die Fragen verständlich gestellt :/ Wäre nett wenn Ihr meine Vorgehensweise kommentiert und mir verbesserungen vorschlägt.

Answer 1

Hi Artur,

Zur 1. Frage

Die letzte Variante ist wohl die beste, wenn es darum geht weiter zu rechnen. Beachte, dass ja auch (x-1) noch berücksichtigt werden muss. "Sauber" aufgeschrieben wäre es also

f'(x) = -2/3x³+2x-4/3 = (x-1) * (-2/3*x^2-2/3*x+4/3)

Und Du wirst im nächsten Schritt nur noch die hintere Klammer anschauen ;).

Zur 2. Frage:

Zur Kontrolle ab damit in die zweite Ableitung. Es heißt ja:

f'(x) = 0 und f''(x) > 0  --> Tiefpunkt

f'(x) = 0 und f''(x) < 0 --> Hochpunkt

Um den Extrempunkt zu bestimmen brauchst Du noch die y-Werte. Dafür dann in die eigentliche Funktion einsetzen (die bitte nicht "Stammfunktion" nennen. Das ist was anderes).

Übrigens hättest Du die Polynomdivision auch für die abc-Formel machen müssen. Da hättest Du später nur beim Vorfaktor von x^2 nicht aufpassen müssen, ist sonst aber dasselbe ;).

Grüße

(Btw. Ergebnisse hab ich nicht kontrolliert. Vertraue Dir da^^)

Comments

Danke !

Nach dem ich x1= 1 und x2= -2 in f''(x) eingesetzt habe, erhalte f '' (x2) = -6 und f '' (x1) = 0

Somit habe ich laut den Kriterien einen Hochpunkt bei der stelle x2.

f'(x) = 0 und f''(x) > 0  --> Tiefpunkt      f'(x) = 0 und f''(x) < 0 --> Hochpunkt

Was ist jetzt aber mit der stelle x1 Ist das ein Hinweis für einen Sattelpunkt ? 

Kannst du mir sagen was ich nun machen sollte ?

Um einen Extrempunkt zu bestimmen brauche ich ja noch die y-Werte. ich setzte die Stellen x1/x2 in die eigentlich Funktion und erhalte :

für x1 folgendes :  F(1) = -1/6*(1)⁴+1*(1)²-4/3*(1)+1/2 = 0

für x2 folgendes :  F(-2) = -1/6*(-2)⁴+1*(-2)²-4/3*(-2)+1/2 = 4,5

Dann habe ich einen Extrempunkt bei  (-2 | 4,5) bei dem es sich um einen Hochpunkt handelt.

---

Zum Hochpunkt: Da ist alles richtig -> H(-2|4,5)

Untersuche noch x₁ = 1 mit der dritten Ableitung. Ist diese ebenfalls 0 hast Du dort eventuell einen Sattelpunkt (Wendepunkte) vorliegen ;). Bzw. man sieht es schon daran, dass Du eine doppelte Nullstelle der ersten Ableitung vorliegen hast^^.