Also das Bild ist selbsterklärend.
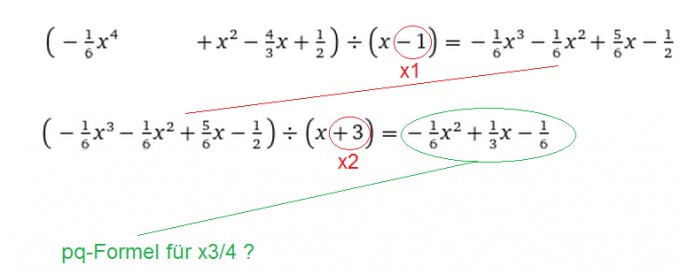
Bevor ich die pq-Formel anwende, forme ich die Funktion natürlich so um, das kein Koeffizient vor dem x^2 mehr steht.
Wenn ich dann die pq-Formel anwende, erhalte ich x3=1 x4=1.
nun Habe ich insgesamt 3 mal die nullstelle 1 raus. Was soll das ^^ ist ja unsinnig wenn ich schreibe Sx1/2/3 = (1|0) oder?
Ich denke: Das Prüfen auf weitere Nullstellen mit der pq-Formel nach einer 2. Polynomdivision ist richtig. Ich muss die Nullstellen aber nicht erneut aufschreiben, wenn ich die bereits ermittelten Stellen wieder als Ergebnis erhalte. (na versteht Ihr's? ^^)
Wäre das falsch ? Und Ist der Grad einer Funktion der Hinweis auf 4 Nullstellen ? Kann ich aus einer Funktion direkt ablesen wie viele Nullstellen es gibt ?