Herleitung der theoretischen Rautiefe beim Drehen

Question

Zu anfangs erstmal für die Leute die eventuell nicht wissen was Drehen ist: https://de.wikipedia.org/wiki/Drehen_(Verfahren)

In der Schule haben wir zurzeit das drehen und die Abhängigkeit von Vorschub und Schneidenradius auf die Theoretische Rauheit bezogen und die Formel
$$R_{th}=\frac{f^2}{8r}$$

wurde dabei genannt, jetzt habe ich mir gedacht das ich mal gucken könnte wieso das ganze so ist, bin aber nicht ganz zufrieden mit meinem Ergebnis, da noch etwas nicht stimmt.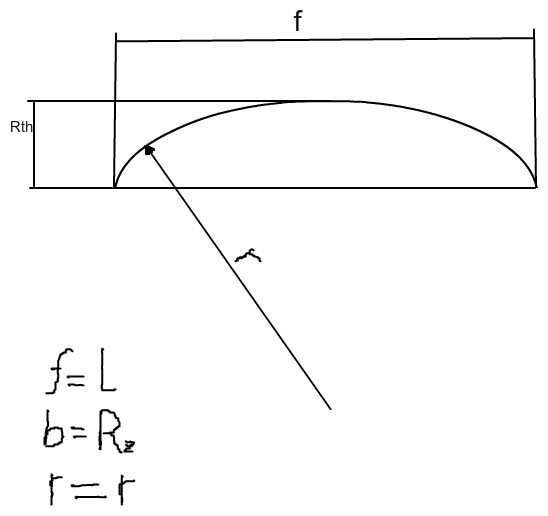

hier ist ein kleines bild wie ich mir das ganze vorstelle.

habe das ganze auf die Kreisabschnittformel reduziert, da hier eig. alles vorkommt was in der Formel der Rauheit  auch vorhanden ist.

die formel für den radius ist hier:

$$r=\frac{b}{2}+\frac{f^2}{8b}$$

wobei ich die Sehnenlänge l mit dem Vorschub f gleichgesetzt habe, da das Rundmaterial sich dreht mit einer bestimmten Umdrehungsfrequenz und der Vorschub in Abhängigkeit zur Umdrehungsfrequenz liegt, daher wird ein bestimmter weg pro Umdrehung zurückgelegt. die breite b habe ich hier mit der Theoretischen Rautiefe gleichgesetzt und der Radius des Kreises entspricht dem Radius der Meißelschneide.

Dann habe ich die Kreisabschnittformel versucht nach der Breite bzw. der Theoretischen Rautiefe umzustellen.

Nach dem austauschen der eigentlichen Formelzeichen sieht die Formel folgendermaßen aus:

$$r=\frac{R_{th}}{2}+\frac{f^2}{8R_{th}}$$

und da bin ich folgendermaßen vorgegangen:

$$r=\frac{R_{th}}{2}+\frac{f^2}{8R_{th}}$$

$$8rR_{th}=4R_{th}^2+f^2$$

$$8rR_{th}-4R_{th}^2=f^2$$

$$R_{th}(8r-4R_{th})=f^2$$

$$R_{th}=\frac{f^2}{8r-4R_{th}$$

das Problem ist, ich werde hier das zweite R_th nicht los :\

würde mich freuen wenn jemand sich das mal anschauen könnte und mir das falls dann noch erforderlich noch erklären könnte
mfg, Subis

Comments

die letzte zeile sollte so aussehen :$$R_{th}=\frac{f^2}{8r-4R_{th}}$$

Answer 1

$$ x(u-vx)=c $$
$$ ux-vx^2-c=0 $$

Comments

was möchtest du mir damit sagen? habe ich das etwa falsch gemacht das ausklammern?

---

Du kommst doch auf ein allgemeine quadratische Gleichung mit Deinen Vorgaben. Vorausgesetzt, Du möchtest nach Rth auflösen, was ich annehme.

---

Ach - du hast ja vorher schon falsch umgestellt !

---

$$ r=\frac b2 + \frac{f^2}{8b} $$
$$ r \cdot 8b =\frac b2 \cdot 8b+ f^2 $$
$$ 8r b =4b^2+ f^2 $$
$$ 0 =4b^2-   8r b     + f^2 $$

und jetzt Mitternachtsformel !

---

oder quadratische Ergänzung:
$$ 0 =4b^2-   8r b     + f^2 $$
$$ 0 =b^2-   2r b     + \left(\frac f2\right)^2 $$
$$ -\left(\frac f2\right)^2 =b^2-   2r b      $$
$$ r^2-\left(\frac f2\right)^2 =b^2-   2r b     + r^2 $$
$$ r^2-\left(\frac f2\right)^2 =(b-   r )^2 $$
$$ \pm \sqrt{r^2-\left(\frac f2\right)^2} =b-   r  $$
$$ r\pm \sqrt{r^2-\left(\frac f2\right)^2} =b  $$

---

ahh ich habe erst versucht die pq formel anzuwenden aber da ich da auch auf zwei Lösungen gekommen bin, kam mir das nicht sehr richtig vor.Ich kann das alles auf jeden fall nachvollziehen aber ich verstehe nicht wieso da nicht die formel, die in meinem tabellenbuch steht, herauskommt :o

Ich bin leider nicht mehr zuhause und schreibe von handy aber ich werde euch nachher mal meine pq formel vorgehensweise davon zeigen wenn ich wieder zuhause bin.

---

sorry, ich habe es am Wochendende echt vergessen, hier trotzdem noch mein Rechenweg:

$$r=\frac{R_z}{2}+\frac{f^2}{8\cdot R_z}$$

$$2r=R_z+\frac{f^2}{R_z \cdot 8}$$

$$8r \cdot R_z=4 \cdot R_z^2+f^2$$

$$R_z^2-2r \cdot R_z+\frac{f^2}{2}$$

$$R_{z1,2}=r \pm \sqrt{r^2-\frac{f^2}{2}}$$

---

Schon bei ersten Umformung ist dir ein Desaster unterlaufen!

Du verdoppelst die linke Seite der Gleichung und den linken Summanden der rechten Seite. Für die Verdopplung des zweiten Summanden der rechten Seite hats nicht mehr gereicht, oder?

---

müsste nur ein abschreib fehler sein der mir unterlaufen ist, sorry :P
der behebt sich doch in den zeilen danach oder nicht?

---

Die zweite Zeile ganz weglassen wäre auch kein Fehler gewesen.

Erst verdoppeln und dann mit 4 malnehmen ...gleich 8 tuts dann auch !

---

und was am Schluss unterm fquadrat steht ... heidenei!

---

das $$\frac{f}{2}^2$$

muss nur $$\frac{f^2}{4}$$ heißen sonst ist aber alles ok oder?

hab jetzt auch schon in der Berufsschule nochmal mit einem Klassenkameraden drüber geredet und ein bisschen gerechnet und nachher unser Ergebnis dem Lehrer gezeigt, er war damit schon zufrieden.

wir sind zu dem Entschluss gekommen so vorzugehen
nach dem auflösen des Binoms haben wir gesagt Rth wird vernachlässigbar klein im Quadrat (da Rth in Bruchteilen von Millimetern angegeben wird) und haben es raus gestrichen und dann haben wir nach dem schritt das Ungefähr-Zeichen eingesetzt.

sieht dann so aus:

$$r^2=\frac{f^2}{4}+r^2-2\cdot r\cdot R_{th}+R_{th}^2$$

$$r^2≈\frac{f^2}{4}+r^2-2\cdot r\cdot R_{th}$$

$$R_{th}≈\frac{f^2}{8 \cdot r}$$