Integralrechnung Stauforscher: Bestimmen Sie die durchschnittliche Fahrzeugdichte auf der gesamten 5-km-Strecke.

Question

Aufgabe:

Stauforscher untersuchen mit verschiedenen Modellen, wie Verkehrsstaus entstehen und wie man sie vermeiden kann. In Rahmen einer solchen Untersuchung wurde die Luftaufnahme einer mehrere Kilometer langen Autobahnstrecke ausgewertet und nach charakteristischen Merkmalen eines Stauendes gesucht. Untersucht wurde insbesondere die Fahrzeugdichte, d.h. die Anzahl der Fahrzeuge pro Meter Fahrbahn, die in Bild dargestellt ist und sich für einen begrenzten Abschnitt durch die Funktion \( f \) mit

\( f(x)=\frac{1}{900} x^{4}-\frac{1}{96} x^{3}+\frac{1}{36} x^{2}+\frac{1}{280} x+\frac{1}{300} \) beschreiben lässt.

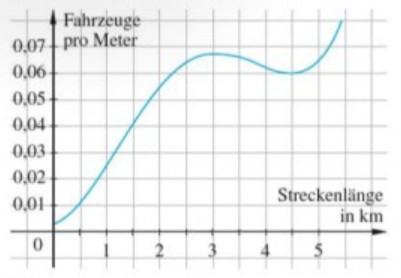
a) Beschreiben Sie qualitativ die Situation auf diesem Autobahnabschnitt.

b) Berechnen Sie die Anzahl der Fahrzeuge, die sich zur Zeit der Luftaufnahme auf den ersten \( 5 \mathrm{~km} \) der Strecke befanden.

c) Bestimmen Sie die durchschnittliche Fahrzeugdichte auf der gesamten 5-km-Strecke.

d) Ermitteln Sie den durchschnittlichen Abstand \( d \) zweier Fahrzeuge zwischen dem ersten und zweiten und zwischen dem dritten und vierten Kilometer der Teststrecke. Treffen Sie hierzu ggf. geeignete Annahmen.

Lösungen:

b) ca. 242 Fahrzeuge
c) ca. 0,048 Fahrzeuge pro Meter
d) Für eine durchschnittliche Fahrzeuglänge von \( 5 \mathrm{~m} \):
1. bis 2. Kilometer: \( d=19,39 \mathrm{~m} \)
3. bis 4. Kilometer: \( d=10,38 \mathrm{~m} \)

Answer 1

Sei \( f(x)=\frac{1}{960}x^4-\frac{1}{96}x^3+\frac{1}{36}x^2+\frac{1}{280}x+\frac{1}{300} \)

Aufgabe (b)
Hier muss das Integral \( 1000\cdot \int_1^2f(x)dx \) berechnet werden.

Aufgabe (c)
Die Dichte berechnet sich aus \( \frac{Anzahl \quad Fahrzeuge \quad auf\quad  5 km}{5000}  \)

Aufgabe (c)
Du musst folgende Gleichung nach x auflösen \( (5+x)\int_1^2 f(x) dx=1000 \) bzw. \( (5+x)\int_3^4 f(x) dx=1000 \) wobei bei Deiner Lösung mit gerundeten Werten gerechnet wurde.