Extremstellen, Wendepunkt, Nullstellen, Wendetangente für f(x)=2/3x³ - 4x² + 6x

Question

ich hatte eine etwas ausführlichere Aufgabe gehabt, nächste Woche schreiben wir auch direkt am Montag eine Leistungskontrolle darüber und ich darf diese auf keinen Fall vermasseln. Wir haben über die Ferien 2 Aufgaben aufbekommen, wo wir jeweils das selbe berechnen sollen. Ich habe eine davon gelöst und würde sehr gerne wissen ob das so stimmt.

Ich habe denke eigentlich alles hinbekommen, ich weiß nur nie richtig wie man die Nullstellen berechnet. Wir können das nicht über die PQ-Formel machen, wir sollen/müssen das durch ausklammern machen.

2/3x³ - 4x² + 6x = 0

Müsste ja sein:

x * (2/3x² - 4x + 6) = 0

Eine Nullstelle wäre somit 0, aber die andere kriege ich dann nie raus.

Naja, hier wären jedenfalls meine anderen Berechnungen

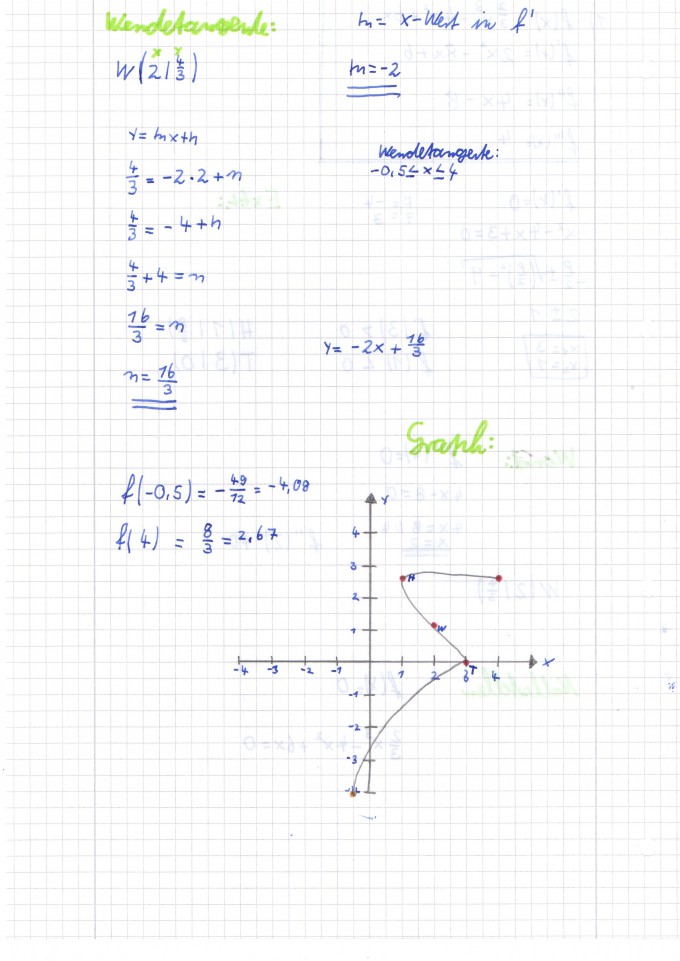
Die Aufgabe war:

Nullstellen, Extrempunkte, Wendepunkte, Wendetangente berechnen

f(x) = 2/3 x³ - 4x² + 6x
Wendetangente: -0,5 < x < 4

Und am Ende den Graphen zeichen, der sieht bei mir irgendwie voll komisch aus. Ich habe wie gewohnt den Hoch- und Tiefpunkt markiert, den Wendepunkt und die Wendetangenten, aber irgendwie ist daraus nur eine merkwürdige Zeichnung geworden.

Sind meine Berechnungen richtig?

Vielen Dank falls sich jemand die Zeit nehmen würde

Answer 1

sieht soweit gut aus, denke ich (abgesehen vom Schaubild).

Zur Nullstellenfrage aber zuerst:

x * (2/3x² - 4x + 6) = 0    |:(2/3)

x * (x^2 - 6x + 9) = 0

x * (x-3)^2 = 0

Wir haben also die binomische Formel erkennen und anwenden können. Damit kann man die Nullstellen nun ablesen ;).

Der Rest hat wie gesagt gepasst.

Die Zeichnung musst Du aber erneut machen. Hochpunkt bedeutet doch, dass das der höchste Punkt ist. Und Du kannst nicht mal nach links und wieder nach rechts hüpfen Oo. Durchlaufe die Punkte von links nach rechts!

Hier ein Beispielbild:

https://www.wolframalpha.com/input/?i=2%2F3*x^3+-+4x^2+%2B+6x

Grüße

Comments

Muss ich beim einzeichnen irgendeine bestimmte Reihenfolge beachten?

---

Ja, von links nach rechts zeichnen (oder andersrum). Sonst aber nicht dass ich wüsste :P.

---

Ich hab einfach keine Ahnung wie :( Das sieht dann bestimmt wieder komisch aus


Habe die 2 Nullstellen jetzt noch eingezeichnet und jetzt sieht es so aus wie auf dem Bild


Weiß nicht wieso sich das Bild beim hochladen immer dreht, kannst du es drehen?

Ich hätte jetzt unten bei dem Punkt bei -4 angefangen, von dort wäre ich zu -3 und dann durch 0|0 und von dort dann immer weiter hoch also erst zu 3x dann zu dem W bei 1 dann zum Hochpunkt und dann zum letzten Punkt (WT) bei ca 2,5

---

Verzeih meine späte Antwort.

Erst die Punkte ins Koordinantensystem eintragen:

Dann die Kurve. Dabei schon etwas geschwungen zeichnen. Nicht so gerade Striche wie bei Dir :P. Sollte dann so aussehen:

Dazu sollte man natürlich eine grobe Vorstellung haben, wie sowas aussieht ;).

Alright?

---

Die Punkte habe ich ja denke auch so, aber wo ist der eine Punkt von (-3|0) also von der Nullstelle? Und die eine Wentetangente mit (4|2,67)

---

Es gibt kein (-3|0).

Und die Wendetangente habe ich nicht eingezeichnet ;). Das überlasse ich Dir. Der Wendepunkt ist aber da. Bei (2|4/3)

---

Sorry für die späte Antwort

Im oberen Beitrag wurde doch aber geschrieben:

NS: (0 / 0), (-3 / 0)

0 ist mir bewusst, aber was ist nun die richtige zweite Nullstelle? Nicht -3?

---

Da war ein Tippfehler drin. Wurde schon moniert^^.

Nun auch gesehen? ;)

---

Wenn ich das alles durch 2/3 teile ist mir bewusst, dass dann folgendes rauskommt:

x * (x² - 6x + 9) = 0

0 ist ja eine Nullstelle

die zweite kriege ich ja nun raus, indem ich die richtige Zahl finde die ich für die beiden x in der Klammer einsetze und dann 0 rauskommt

Das muss ich ja jetzt irgendwie durch probieren machen, richtig?

Du hast ja noch x * (x-3)² = 0 stehen

Aber wie kommst du darauf?

Dort müsste dann 3 rein, stimmts?

Also sind die Nullstellen 0 und 3

Habe auch danach nochmal deine Zeichnung angeguckt, dort hast du ja auch einen Punkt auf der 3

Nur muss ich wissen wie ich auf x * (x-3)² = 0 komme, damit würde die zweite Nullstelle dann ja einfach sein zu berechnen.

, dass du mir alle meine Fragen beantwortest.

---

Morgen ;).

Du hast ja noch x * (x-3)² = 0 stehen

Genau, da habe ich die zweite binomische Formel erkannt. Sollte man mit der Zeit erkennen können. Wenn nicht, kannst Du aber auch x^2-6x+9 = 0 mittels der pq-Formel lösen.

Richtig ist aber, dass Du in die Klammer (x-3)^2 eine Zahl einsetzen musst, so dass diese 0 ergibt. Das wäre für x = 3 der Fall.

---

Dann werde ich es denke lieber mit der PQ-Formel machen

Würde ich x² - 6x + 9 = 0 jetzt mit der PQ-Formel berechnen, müsste also 3 und 0 rauskommen, oder?

---

Nein, dann müsste da 3 und 3 rauskommen. Probiers mal aus ;).

Answer 2

Die Extrempunkte sind korrekt berechnet und die Wendepunkte auch. Die Wendetangente ist auch korrekt.

Wenn ihr bei den Nullstellen keine pq-Formel anwenden sollt, dann kann man die Gleichung der Funktion so umstellen, dass man sie dann leicht erkennen kann. Das heist meist ausklammern und binomische Formel.

2/3x³ - 4x² + 6x = 0 | :2

1/3x³ - 2x² + 3x | *3

x³ - 6x² + 9x  = x*(x² + 6x + 9) = x*(x + 3)²

x₁= 0, x₂= -3

NS: (0 / 0), (-3 / 0)

Bei deinem Graphen hast du Extrempunkte und Wendepunkt korrekt eingezeichnet, dir fehlen nur die Nullstellen. Dann hast du nur die Punkte falsch miteinander verbunden.
Als Tipp, wenn du irgendwo einen Hochpunkt hast, dann muss da so etwas wie eine Bergkuppe sein, die du direkt leicht hinzeichnen kannst, bei einem Tiefpunkt befindet sich ein Tal, das du auch direkt leicht hinzeichnen kannst. Die Hoch und Tiefpunkte laufen bei solchen Funktionen nie spitz zu sondern immer rund.
Wenn du die Punkte einfach so nochmal neu verbindest, dann hast du schon fast die Kurve und mit den Nullstellen ergibt sich der restliche Verlauf dann fast von selbst.

An sonsten ist doch schon alles ziemlich ordentlich. Ein wenig durcheinander an einigen Stellen aber die Ergebnisse stimmen.

Comments

Hi,
die binomische Formel bzw. der Ausklammerschritt davor ist falsch.

x³ - 6x² + 9x  = x*(x² + 6x + 9) = x*(x + 3)²

Da muss es je nen Minus sein.

Grüße

---

Stimmt, danke für den Hinweis