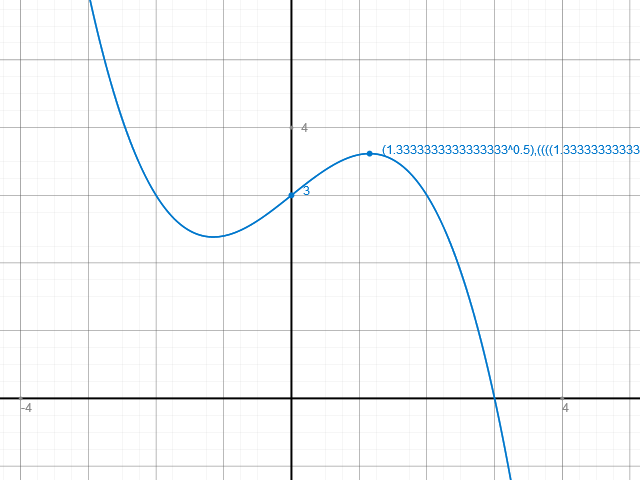
Extremstellen, Wendepunkte und Nullstellen für f(x)=-1/5*x^3+4/5*x+3

Question

ich habe schonmal so eine ähnliche Frage gestellt:
https://www.mathelounge.de/159871/extremstellen-wendepunkt-nullstellen-wendetangente

Ich habe nun auch die zweite Aufgabe gelöst, siehe Bilder

Ich würde wieder sehr gerne wissen, ob ich das richtig gemacht habe. Ich vermute nämlich nicht.

Ich habe ein paar Fragen, bezüglich:

Extremstellen: Ist es normal bzw. von mir richtig gerechnet wurden, dass am Ende 4/3 und 0 rauskommt? Der Hochpunkt wäre ja (4/3 97/27)

Gibt es einen Tiefpunkt? Da war ich mir nicht sicher. Der erste Wert ist ja 0, wenn ich diesen in f'(x) einsetze, kommt logischerweise 0,8 raus.

Wendepunkt:

Dort musste ich ja f''(x) = 0 rechnen.

Da oben nur -6,5x steht, kommt da ja auch 0 raus, oder?

Gibt es da nun keinen Wendepunkt oder ist der Wendepunkt W(0|0) ?

Nullstellen:

f(x) = 0

Dort habe ich erstmal alles durch -1/3 gerechnet, damit ich am Anfang auf x² komme und habe dann
x² - 4x - 15 = 0 mit der pq-Formel berechnet.

Ich komme wie ihr sehen könnt am Ende auf 2 ± √19

Wenn ich die Wurzel aus 19 ziehe, kommt eine Kommazahl raus, das kann doch nicht stimmen, oder?

Bei meiner alten Frage wo ich oben bereits den Link eingefügt habe, wurde mir bei den Nullstellen gesagt, dass nach der Berechnung mit der pq-Fomel 3 und 3 als Nullstelle rauskommt, müssen dann jetzt nicht wieder die 2 selben Nullstellen rauskommen?

Denn eine Nullstelle ist ja 0, wegen dem x * vor der Klammer.

Hier wäre dann der Rest (Wendetangente und Graph)


Vielen Dank wenn mir jemand meine Fragen beantworten kann.

Answer 1

Da sind doch so einige Fehler drin. pq-Formel solltest du dir anschauen.

Funktion und Ableitungen

f(x) = - 1/5·x^3 + 4/5·x + 3

f'(x) = - 3/5·x^2 + 4/5

f''(x) = - 6/5·x

f'''(x) = - 6/5

Symmetrie

Keine untersuchte Symmetrie.

Verhalten im Unendlichen

lim (x → -∞) f(x) = ∞

lim (x → ∞) f(x) = -∞

y-Achsenabschnitt f(0)

f(0) = 3

Nullstellen f(x) = 0

- 1/5·x^3 + 4/5·x + 3 = 0

x = 3

Polynomdivision

(- 1/5·x^3 + 4/5·x + 3) : (x - 3) = - 1/5·x^2 - 3/5·x - 1

- 1/5·x^2 - 3/5·x - 1 = 0

Keine weiteren Lösungen

Extrempunkte f'(x) = 0

- 3/5·x^2 + 4/5 = 0

x = - 2/3·√3 = -1.15 ∨ x = 2/3·√3 = 1.15

f(- 2/3·√3) = 3 - 16/45·√3 = 2.38 --> TP(-1.15 | 2.38)

f(2/3·√3) = 16·√3/45 + 3 = 3.62 --> HP(1.15 | 3.62)

Wendepunkte f''(x) = 0

- 6/5·x = 0

x = 0

f(0) = 3 --> WP(0 | 3)

Answer 2

Extremstellen

Bei den Extremstellen hast du die pq-Formel falsch angewendet. Du hast dort kein p sondern nur ein q. Bei p steht immer ein x dabei. q steht alleine. Richtig eingesetzt kommst du für deine x-Werte auf x_1,2=±√(4/3)

Verstehe aber nicht, weshalb du überhaupt die pq-Formel benutzt. Wenn du -4/3 auf die andere Seite bringst, steht da x² = 4/3. Dann kannst du einfach die Wurzel ziehen und bist fertig.

Wendepunkt

notwendige Bedingung: f ''(x) = 0 und f '''(x)≠0

Du hast für f ''(x)=0  x=0 herausbekommen, jetzt musst du nur noch prüfen, ob die 3. Ableitung bei x=0 ungleich null ist. f'''(0) = -6/5 ≠ 0 --> WP

Um den y-Wert des WP zu bekommen, setzt du deinen x-Wert x=0 in deine Ausgangsgleichung f(x) ein.

f(0) = 3

WP(0/3)

Nullstellen

Keine Ahnung weshalb du da irgendwas durch -1/3 teilst. Um die Brüche wegzubekommen einfach mit -5 multiplizieren, dann hast du

x³ -4x -15 = 0

Hier kannst du nichts ausklammern und auch keine pq-Formel anwenden. pq-Formel nur wenn höchster Exponent 2 ist hier steht aber x³.

Hier kannst du nur raten. x=3 ist eine Nullstelle

Polynomdivision (x³ -4x -15) / (x-3) = x²+3x+5

Jetzt kannst du die pq-Formel anwenden um zu prüfen, ob es noch weitere Nullstellen gibt.

-3/2 ±√(9/4 - 20/4) , Wurzel ist negativ, deshalb keine Lösung

Damit ist deine einzige Nullstelle bei x=3

NS (3 / 0)

Comments

Keine Ahnung weshalb du da irgendwas durch -1/3 teilst. Um die Brüche wegzubekommen einfach mit -5 multiplizieren, dann hast du

Schau mal hier bei der Antwort von Unknown:
https://www.mathelounge.de/159871/extremstellen-wendepunkt-nullstellen-wendetangente

Dort hatte ich:

x * (2/3x² - 4x + 6) = 0 |:2/3

x * (x² - 6x + 9) = 0

Deshalb habe ich es bei meiner Aufgabe von diesem Beitrag hier durch 1/5 gerechnet weil ich es bei der anderen durch 2/3 rechnen sollte. Und dann hat er mir gesagt "kannst Du aber auch x²-6x+9 = 0 mittels der pq-Formel lösen."

also habe ich es da auch gemacht

---

Du kannst doch aber nicht immer alles einfach blind durch 1/3 teilen. Du musst dir doch ansehen, welche Brüche genau du weghaben willst. In dieser Funktion hast du -1/5 vor x² stehen. Da kannst du doch nicht durch 1/3 teilen. Das bringt doch nichts.

Ich würde dir auch raten, nicht zu teilen, sondern mit dem Kehrwert zu multiplizieren um Brüche wegzubekommen. Hier willst du Brüche mit 5 im Nenner wegbekommen und zusätzlich noch das Minus Zeichen bei x³ wegkriegen. Kehrwert von 1/5 ist 5. Also multiplizierst du den Ausdruck mit -5 und das Miuszeichen und die Brüche sind weg.

Zur pq-Formel, klar kannst du das, was du jetzt gerade geschrieben hast, mit pq-Formel lösen, da steht ja auch als höchste Potenz x² und nicht x³ wie in der Aufgabe oben. Bei x³ kannst du keine pq-Formel anwenden. Schau dir am besten noch mal ganz genau die pq-Formel an. Und auch wann man die benutzen darf und wann nicht.

Answer 3

Die anderen beiden haben dir ja schon Antworten
gegeben bzw. deine Berechnungen überprüft.

Ein Fehler bei dir lag bei

- 3/ 5 x^2 + 4 / 5 = 0
x^2 - 4 / 3 = 0
( hier ist keine pq-Formel notwendig bzw. falsch, sondern )
x^2 = 4 / 3
x = ± √ ( 4 / 3 )

x = + √ ( 4 / 3 )
x = - √ ( 4 / 3 )

Jetzt hättest du eine PROBE machen können und das Ergebnis
in die Ausgangsgleichung einsetzen können. Wird die Ausgangs-
gleichung wahr stimmt das Ergebnis.

[ - 3/ 5 x^2 + 4 / 5 = 0  ] und  [ x = + √ ( 4 / 3 ) ]
- 3/ 5 *  [ + √ ( 4 / 3 )]^2 + 4 / 5 = 0
-3/5 * 4/3 + 4 / 5 = 0  | stimmt

[ - 3/ 5 x^2 + 4 / 5 = 0  ] und  [ x = - √ ( 4 / 3 ) ]
- 3/ 5 *  [ - √ ( 4 / 3 )]^2 + 4 / 5 = 0
-3/5 * 4/3 + 4 / 5 = 0  | stimmt

Dein Ergebnis mit x = 0

[ - 3/ 5 x^2 + 4 / 5 = 0  ] und  [ x = 0 ]
- 3/ 5 *  0^2 + 4 / 5 = 0
 4 / 5 = 0 
stimmte also nicht.