Zunächst mache ich eine grobe Skizze.
Rechnung folgt danach.
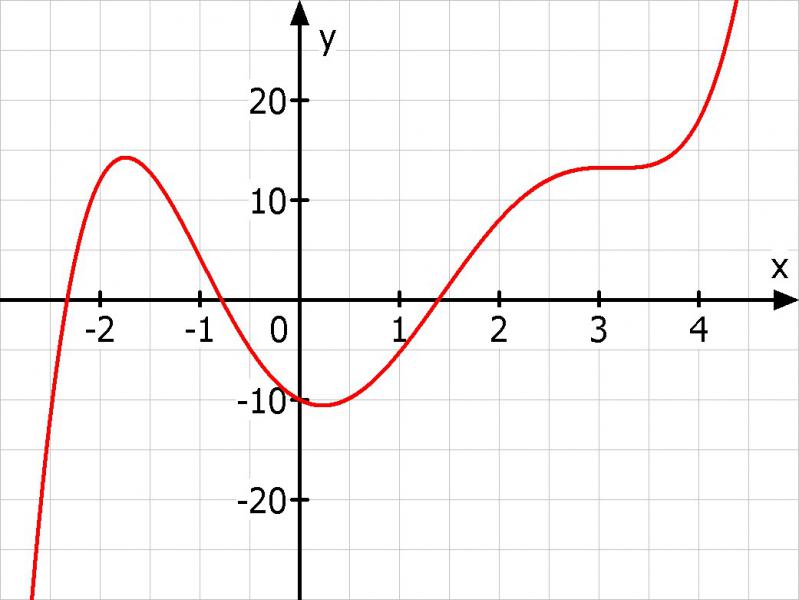
f(x) = 0.25·x^5 - 1.5·x^4 + 11·x^2 - 5·x - 10 mit x in km und f(x) in m; -3 < x < 4
f '(x) = 1.25·x^4 - 6·x^3 + 22·x - 5
Im linken teil des profils befindet sich eine insel, rechts ist festland.
wie lang und wie hoch ist die insel im profil?
Nullstellen f(x) = 0
Ungünstigerweise gibt es keine ganzzahligen Nullstellen sodass wir ein Näherungsverfahren wie das Newtonverfahren benutzen müssen
xn+1 = xn - (0.25·xn^5 - 1.5·xn^4 + 11·xn^2 - 5·xn - 10)/(1.25·xn^4 - 6·xn^3 + 22·xn - 5)
x = -2.329831240
x = -0.7818562489
x = 1.389943003
-0.7818562489 - (-2.329831240) = 1.548 km ist die Insel lang
Extremstelle f '(x) = 0
1.25·x^4 - 6·x^3 + 22·x - 5 = 0
Auch hier haben wir nicht mehr Glück und finden auch keine Ganzzahligen Nullstellen. Die Nullstellen sind mit dem Newtonverfahren
x = -1.743623468 ; y = 14.26707796
x = 0.2304502776 ; y = -10.57213884
x = 3.060170837 ; y = 13.25700140
x = 3.253002353 ; y = 13.23557948
Die Insel ist 14.27 m hoch.
wie tief ist das meer zwischen insel und festland?
Das Meer ist gerade mal 10.57 m tief.