Aufgabe (Additionstheoreme fur Sinus und Kosinus):
Wir betrachten zwei Dreiecke \( A B C \) und \( A C D \) derart, dass die beiden Winkel \( \angle A C B \) und \( \angle A D C \) rechte Winkel sind. Wir setzen \( \alpha:=\angle B A C \) und \( \beta:=\angle C A D \). Es gelte \( 0 \leq \alpha, \beta \) und \( \alpha+\beta<\frac{\pi}{2} \).
Zeigen Sie durch elementargeometrische Betrachtungen, dass
$$ \sin (\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta \quad \text { und } \quad \cos (\alpha+\beta)=\cos \alpha \cos \beta-\sin \alpha \sin \beta $$
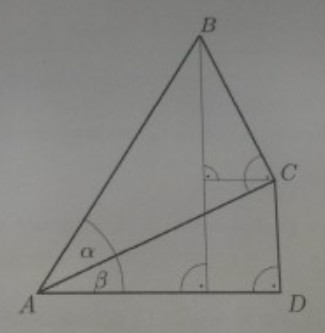
Hinweis: Da die Größe der Winkel unter Streckungen gleich bleibt, können Sie annehmen, dass die Strecke \( A B \) die Länge 1 hat. Bestimmen Sie alle Winkel und Längen in der Skizze.