Gegeben ist die Funktion:

Question

ƒ(x) = (3x + 6) e^-x

bestimmen sie Definitionsmege und die Nullstellen von f,

bestimmen sie Extrem und wendpunkte von f !

geben sie ein Gleichung der Wendetangente an.

berechnen Sie Lim x→-∞ ƒ(x) und Lim x→∞ ƒ(x) !

Skizzieren Sie den Graphen der Funktion F!

Answer 1

f(x) = (3x+6)e^{-x}

f'(x) = -(3x+3)e^{-x}

f''(x) = 3xe^{-x}

f'''(x) = (-3x+3)e^{-x}

mittels der Produkt- und Kettenregel

Defintionsmenge: D = R, da keine Problemstelle

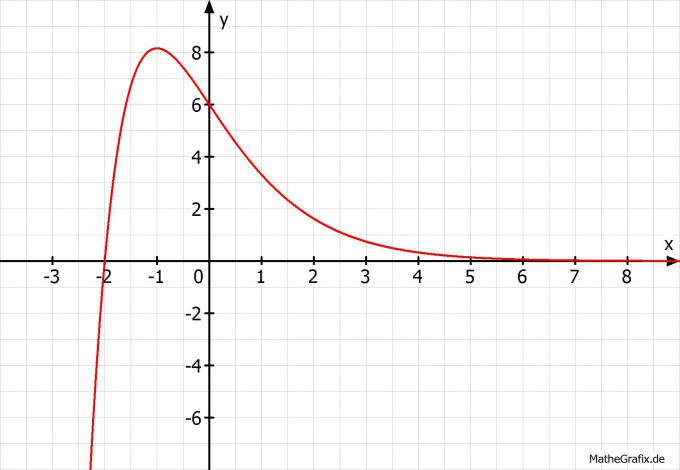
Nullstelle: f(x) = 0 = (3x+6)e^{-x}

Die e-Funktion wird nie 0, also (3x+6) = 0 -> x = -2

Extrema:

f'(x) = 0 = -(3x+3)*e^{-x}

Wieder: e-Funktion wird nie 0: -(3x+3) = 0 -> x = -1

Mit der zweiten Ableitung kontrollieren und in f(x) einsetzen:

H(-18,155)

Wendepunkt:

f''(x) = 0 = 3x*e^{-x}

x = 0

Mit dritter Ableitung überprüfen und in f(x) einsetzen:

W(0|6)

Wendetangente: Geht durch W(0|6) und hat die Steigung f'(0) = -3

Also: y = -3x + 6

(wobei 6 der y-Achsenabschnitt direkt durch W abzulesen ist)

Verhalten:

lim x→-∞ ƒ(x) = -∞, da die e-Funktion gegen ∞ geht und 3x für das negative Vorzeichen sorgt

lim x→∞ ƒ(x) = 0, da die e-Funktion 0 wird

Schaubild

Grüße