Ich habe schon die Aufgaben a und b gelöst . Jedoch komme ich bei der c nicht ganz weiter . und die Aufgaben d , e und f verstehe ich leider gar nicht.
Abiturprüfung 2007, Mathematik, Leistungskurs - Aufgabenstellung:
Um die Wasserstände eines Flusses vorherzusagen, kann man versuchen, die Durchflussgeschwindigkeit des Wassers an einer bestimmten Stelle des Flusses mit Hilfe geeigneter Funktionen zu beschreiben.
Solche näherungsweise Beschreibungen der Durchflussgeschwindigkeiten seien z.B. gegeben durch die Funktionenschar
\(f_a \text{ mit } f_a(t)=\frac{1}{4}t^3-at^2+a^2t, \quad a > 0\)
a) Berechnen Sie abhängig vom Parameter a, zu welchen Zeitpunkten gerade kein Wasser durch den Fluss fließt.
b) Ermitteln Sie in Abhängigkei von a, zu welchen Zeitpunkten die Durchflussgeschwindigkeit ein relatives Maximum bzw. Minimum annimmt, und berechnen Sie diese Funktionswerte.
c) Ermitteln Sie in Abhängigkeit von a, wann die Durchflussgeschwindigkeit besonders stark absinkt und berechnen Sie ihren Wert zu diesem Zeitpunkt.
In der nachstehenden Abbildung sind die Graphen der Funktionen f2 und f3 dargestellt.
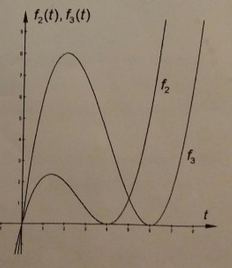
d) Begründen Sie, warum kein Punkt der Funktionsgraphen von fa im Bereich t ≥ 0 unterhalb der t-Achse liegt und inwiefern dies mit dem zugrunde liegenden Sachverhalt vereinbar ist.
Geben Sie das Verhalten von fa für t → \(\infty\) an und begründen Sie, ob die Funktionen auch nach den ersten 8 Monaten noch eine sinnvolle Beschreibung der Durchflussgeschwindigkeit liefern.
e) Ermitteln Sie für a = 3, wie viel Liter Wasser in den ersten sechs Monaten durch den Fluss fließen.
f) Betrachten Sie nun zwei verschiedene Funktionen \(f_{a1}\) und \(f_{a2}\). Bestimmen Sie den Zeitpunkt t0, zu dem für beiden Funktionsannahmen (seit t = 0) genau gleich viel Wasser durch den Fluss geflosen wäre.
Bitte um Hilfe liebe Mathematiker .