Text erkannt:
Aufgabenstellung:
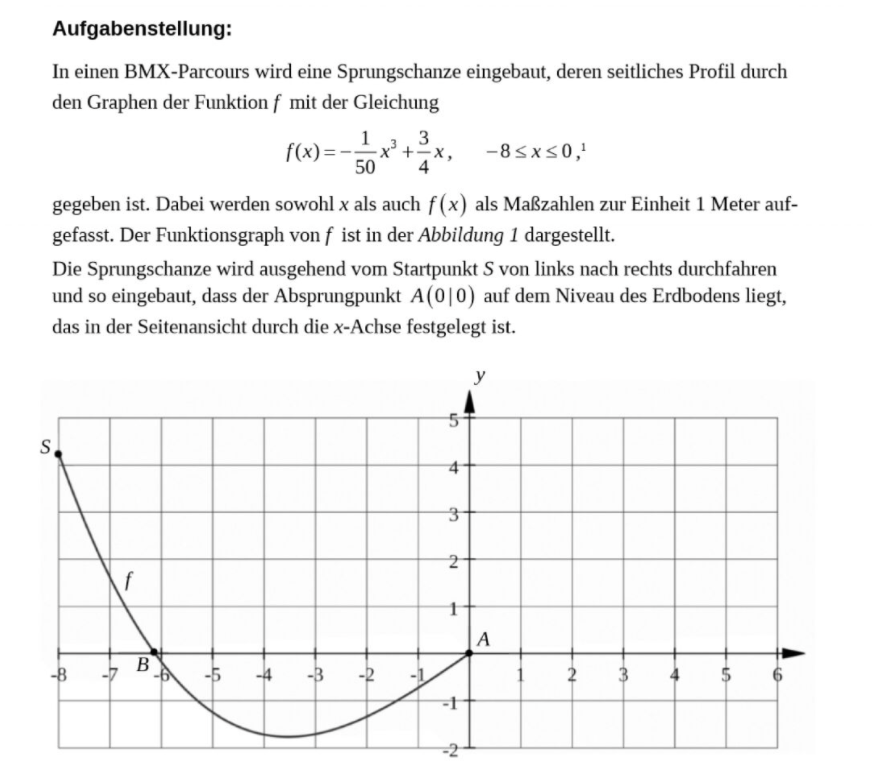
In einen BMX-Parcours wird eine Sprungschanze eingebaut, deren seitliches Profil durch den Graphen der Funktion \( f \) mit der Gleichung
\( f(x)=-\frac{1}{50} x^{3}+\frac{3}{4} x, \quad-8 \leq x \leq 0,1 \)
gegeben ist. Dabei werden sowohl \( x \) als auch \( f(x) \) als Maßzahlen zur Einheit 1 Meter aufgefasst. Der Funktionsgraph von \( f \) ist in der Abbildung 1 dargestellt.
Die Sprungschanze wird ausgehend vom Startpunkt \( S \) von links nach rechts durchfahren und so eingebaut, dass der Absprungpunkt \( A(0 \mid 0) \) auf dem Niveau des Erdbodens liegt, das in der Seitenansicht durch die \( x \)-Achse festgelegt ist.

Text erkannt:
b) (1) Bestimmen Sie rechnerisch die Koordinaten des tiefsten Punktes T des Sprungschanzen-Profils.
(2) Berechnen Sie den Winkel gegen die Horizontale, unter dem die BMX-Fahrer im Punkt A die Schanze tangential verlassen.
(12 Punkte)

Text erkannt:
d) Um den BMX-Fahrern nach dem Sprung eine weichere Landung zu ermöglichen, soll rechts vom Punkt \( A \) im Bereich \( 0 \leq x \leq 5 \) ein Aufsprunghügel angelegt werden, dessen seitliches Profil durch den Graphen einer ganzrationalen Funktion 3. Grades \( h \) zu modellieren ist. Dieses soll im Punkt \( A \) ohne Knick an das Profil der Sprungschanze anschließen und im Punkt \( D(5 \mid 0) \) ebenfalls ohne Knick in die waagerechte Erdoberfläche übergehen.
(1) Geben Sie die Bedingungen an, die die Funktion h erfüllen muss, und leiten Sie daraus eine Gleichung dieser Funktion h her (siehe Abbildung 2).
[Zur Kontrolle: \( h(x)=\frac{3}{100} x^{3}-\frac{3}{10} x^{2}+\frac{3}{4} x \) ]
(2) Bestimmen Sie die Stelle, an der der durch den Graphen der Funktion h modellierte Aufsprunghügel die betragsmäßig größte Steigung hat.
Aufgabe:
abiturprüfung 2013 .Ich wäre euch so dankbar wenn ihr die lösungen habt oder ansätze zu jeder aufgabe habt
Problem/Ansatz:
spezifisch brauche ich hilfe bei b) und d) danke schonmal ihr rettet mein hintern.