ich habe mir deine Überlegungen nicht angeschaut und sehe
das Ganze mehr vom Physikalischen/Statik.
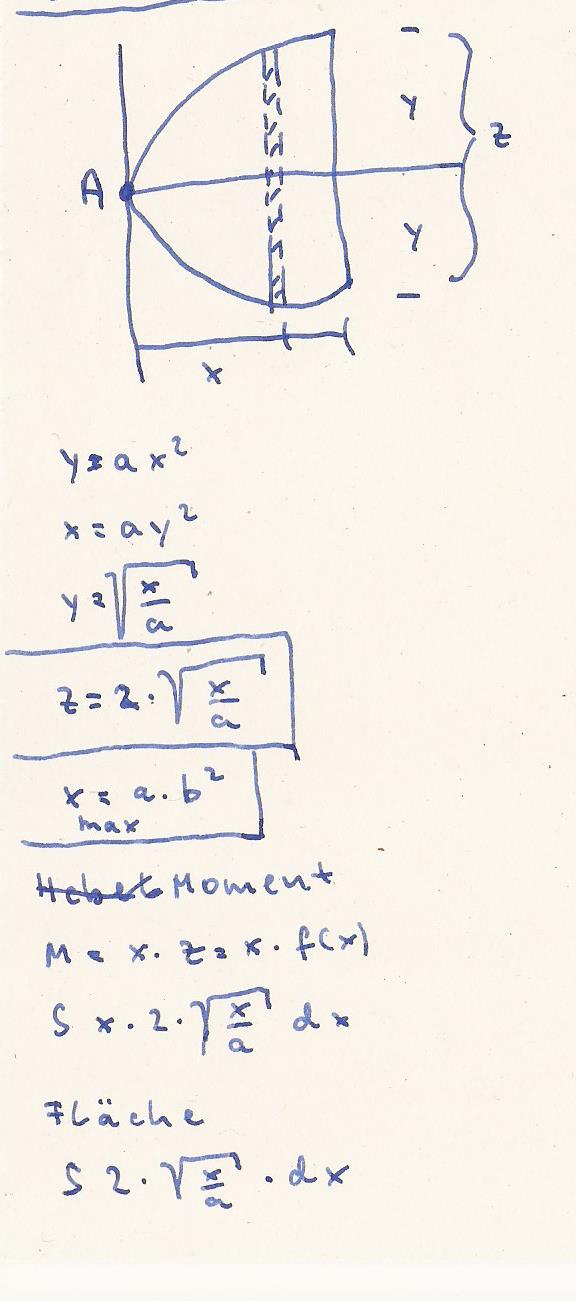
Ich habe die Parababel um 90 ° gedreht und
die Umkehrfunktion gebildet
Wobei wegen der Wurle nur der positive Wert
herauskommt. Dann z = 2 * y
Punkt A ist der Drehpunkt. Es entstehen Momente
Kraft mal Hebelarm : M = x * z
Die Stammfunktion muß noch gebildet werden.
Die Integratiosngrenzen sind : von 0 bis x(max)=a*b^2.
Dann muß die Fläche berechnet werden.
∫ 2 * √ (x/a) dx. Mit denselben Integrationsgrenzen.
xs ist die Länge ( Hebelarm ) bis zum Schwerpunkt.
M = Fläche * xs
Das Ganze ist relativ physikalisch.
Fiel mir spontan so ein.
mfg Georg