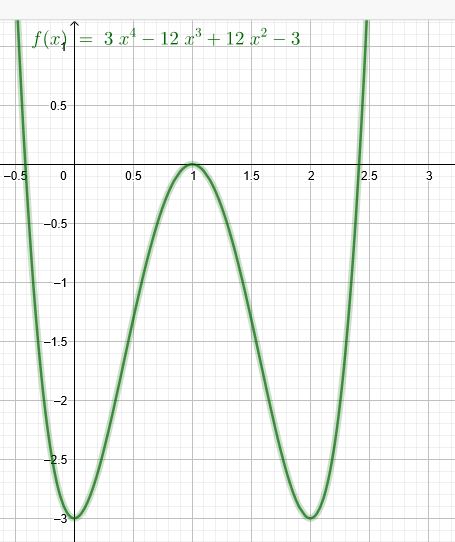
1) Gegeben sei die Funktion f mit \(f(x) =3 x^4 -12x^3 +12 x^2 -3\)
a) Bestimmen Sie die Nullstellen , die Lage Art der Extremwerte sowie die Lage der Wendepunkte der Funktion f.
Nullstellen:
Probieren mit \(x=1\)
\(f(1) =3 -3=0\) Somit ist bei \(x=1\) eine Nullstelle.
Weiter mit Polynomdivision:
\((3 x^4 -12x^3 +12 x^2 -3):(x-1)=3x^3-9x^2+3x+3\)
Probieren mit \(x=1\)
Wieder ist hier eine Nullstelle, sie ist doppelt und somit auch eine Extremstelle.
Nun Polynomdivision mit \((x-1)^2=x^2-2x+1\)
\((3x^3-9x^2+3x+3):(x^2-2x+1)=3x^2-6x-3\)
Mit den bekannten Mittel lassen sich nun die beiden weiteren Nullstellen berechnen.
\(3x^2-6x-3=0\)
\(x^2-2x=1\)
\((x-1)^2=2|±\sqrt{~~}\)
1.)
\(x-1=\sqrt{2}\)
\(x_1=1+\sqrt{2}\)
2.)
\(x-1=-\sqrt{2}\)
\(x_2=1-\sqrt{2}\)
Extremwerte:
Eine Extremstelle ist schon bei \(x=1\) gefunden worden.
\(f'(x) =12 x^3 -36x^2 +24x \)
\(12 x^3 -36x^2 +24x=0 \)
\( x^3 -3x^2 +2x=0 \)
\( x(x^2 -3x +2)=0 \) Satz vom Nullprodukt:
\(x_2=0 \) \(f(x) = -3\)
\( x^2 -3x=-2 \)
\( (x -1,5)^2=-2+1,5^2=0,25|±\sqrt{~~} \)
1.)
\( x -1,5=0,5 \)
\( x_2 =2 \) \(f(2) =3 \cdot 16 -12\cdot 8 +12\ cdot 4 - 3=-3\)
2.)
\( x -1,5=-0,5 \)
\( x_3=1 \) siehe auch bei den Nullstellen
Art der Extremwerte:
\(f''(x) =36 x^2 -72x +24 \)
\(f''(0) =24>0 \) Minimum
\(f''(1) =36 -72 +24=-12<0 \) Maximum
\(f''(2) =36\cdot 4 -72\cdot 2 +24=24 >0 \) Minimum
Wendestellen:
\(36 x^2 -72x +24=0 \)
\( x^2 -2x =-\frac{2}{3} \)
\( (x -1)^2 =-\frac{2}{3}+1=\frac{1}{3} \)
Weiter ausrechnen.
Die Wendepunkte lassen sich auch berechnen.
Es ist schon spät. Morgen suche ich den Fehler!
