Finden Sie alle Lösungen der Gleichung cos(3x) = 0,5

Question

ich habe folgendes Problem:

Die Aufgabenstellung lautet:

"...Finden Sie alle Lösungen der Gleichung cos(3x) = 0,5

a) in ganz ℝ

b) im Intervall [0;π]

c) im Intervall (π;2π]..."

Nun meine Frage:

Ich habe dann nach X aufgelöst, also:

cos(3x) = 0,5

3x = 60

x = 20

Ab jetzt weiß ich nicht mehr weiter!

Was will der Aufgabensteller von mir, wenn er schreibt: "Ich soll alle Lösungen finden"?

!

LG

Answer 1

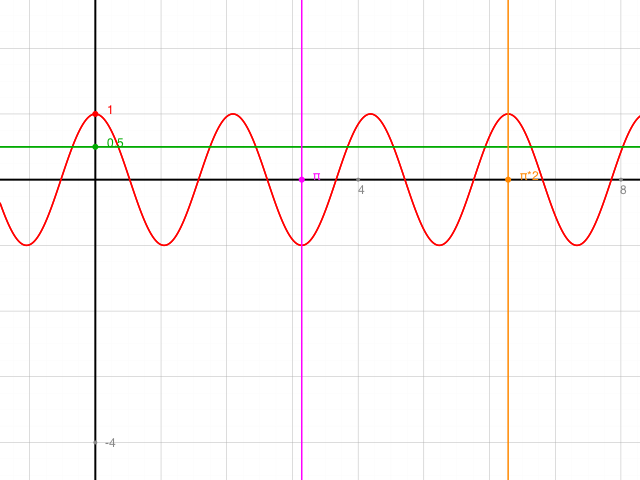
Der Fragesteller will von dir die Schnittstellen der abgebildeten Kurven y = cos(3x) und y = 0.5.

Bei a) will er alle unendlich vielen Lösungen, die es überhaupt gibt . Da musst du dann ein zwei Formeln mit k Element Z hinschreiben.

bei b) musst du nur die angeben, die zwischen der y-Achse und der lila Linie liegen. 

bei c) dann die zwischen der lila Linie und der gelben Linie.

Beachte: 

cos(3x) = 0,5        |

3x = arccos(0.5) 

x = 1/3 * arccos(0.5) 

x = 1/3 * 60° = 20° = π/9

Nun betrachtest du den Graphen und benutzt dortige Symmetrien, um die andern Lösungen anzugeben. Offensichtlich solltest du die x-Wert in Bogenmass angeben. Am besten

b) x1 = π/9 , x2 = 2π/3 - π/9 = 5π/9, x3 = 2π/3 + π/9 = 7π/9.

c) x1 = 4π/3 - π/9 = 11π/9, ....

a) verallgemeinere b) und c).

Comments

Ich danke dir, deine Antwort ist die Beste! Super erklärt!

Nun wird es mir klar, hab alles verstanden! ;)

Answer 2

COS(3·x) = 0.5

3·x = k·2·pi ± ARCCOS(0.5) = k·2·pi ± pi/3

x = k·2/3·pi ± pi/9

Answer 3

Ich habe dann nach X aufgelöst, also:

cos(3x) = 0,5

3x = 60°     Das ist ja Gradmaß!

Da du aber offensichtlich im Bogenmaß rechnen sollst,

wäre das 3x=pi/3 oder aber   3x = 5pi/3

und in ganz IR dann  weil nach jeweils 2pi sich die Werte wiederholen

3x=pi/3 + n*2pi oder aber   3x = 5pi/3 + n*2pi

also für das x

x= pi/9 + n* 2pi/3   oder  x= 5pi/9 + n* 2pi/3 

im Int von 0 bis pi liegen davon 

    pi/9   und pi/9 +  2pi/3  = (7/9)pi    und 5pi/9  

etc.