Wie kann man hier die gegenseitige Lage der Geraden beschreiben?

Question

Ich bin mir bei folgender Aufgabe unsicher bzw. habe keinen wirklichen Ansatz:

von folgender Aufgabe soll die gegenseitige Lage beschrieben werden:

f(x) = -0,5x^3 +2x
g(x) = -0,5 ( x^3+2x^2+x)

Ich habe bis jetzt:

F ' (x) = -1,5x^2 +2
g ' (x) = -1,5x^{2} -2x-0,5

wenn ich die beiden Gleichsetze (um eventuell gleiche Steigungen zu beweisen)
komme ich bis

-x^{2} - 4/3x = 1/3


LG

Comments

Hi Norgemathics,

f(x) = -0,5x³ +2x

und

g(x) = -0,5 ( x³+2x²+x)

sind keine Geraden, sondern Parabeln!

Du kannst den Schnittpunkt der Graphen berechnen, aber viel mehr m. E. nicht.

Besten Gruß

---

Ähm, jaa ich meinte eigentlich Graphen, sorry.
Kann man den gar nichts zur gegenseitigen Lage sagen? EVtl dass der Wendepunkt von g(x) gleich dem Sattelpunkt von f(x) ist?

---

Ich habe Dir mal eine kleine Skizze gemacht:

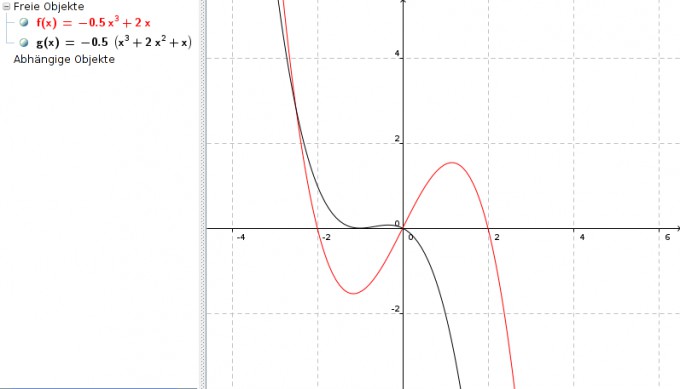
Du kannst also durch Gleichsetzen der beiden Funktionsgleichungen einfach die Schnittstellen berechnen.

Außerdem sieht es so aus, dass der Schnittpunkt (0|0) gleichzeitig der Wendepunkt von f(x) ist - auch das muss sich ja unschwer errechnen lassen (f''(x) = 0).

Besten Gruß

---

Keine Ursache, gern geschehen! :-)

---

Hi Brucybabe ich habe vor einer halbrn stunde meine Aufgaben geschickt und his jetzt keine Antwort

Ich sitz hier lange und habe keine antwort

Könntest du mir meine Aufgaben beantwortrn danke

---

Hi princeess,

ist soeben geschehen :-D

Answer 1

die Funktionen schneiden sich 2 mal.
Ansonsten gibt es keine Auffälligkeiten.

mfg Georg

Comments

Danke, ich soll aber rechnerisch Vermutungen über f(x) und g(x) beweisen..
Also reicht es f(x) mit g(x) gleichzusetzen nehme ich an.

---

Berechnung des Schnittpunkts f ( x ) = g ( x ).
x = -2.5 , x = 0
Vielleicht kannst du noch überprüfen ob die
Funktionen im Schnittpunkt x = 0
orthogonal aufeinander stehen
f ´( 0 ) = - 1 / g ´( 0)
Von der Skizze her wäre es möglich.

---

Meine Vermutung ist richtig.