Dreidimensionale Körper berechnen: Volumen und Oberflāche des Kegels, zylinderförmige Cremedose, Schachtel

Question

Aufgabe 1:

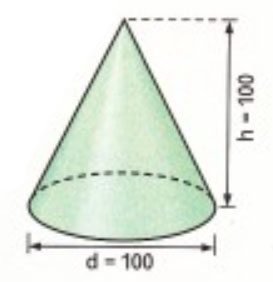
a) Berechne Volumen und Oberflāche des Kegels (Maße in cm).

b) Stimmt es, dass ein Kegel mit h = 100 cm und d = 80 cm 80 % des Volumens vom Kegel aus a) hat? Begründe.

Aufgabe 2:

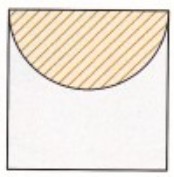
Das Bild zeigt den Querschnitt durch eine handelsübliche zylinderförmige Cremedose. Nur der schraffierte Teil ist gefüllt. Wie viel Prozent der Dose ist das etwa? Beschreibe deinen Lösungsweg.

Aufgabe 3:

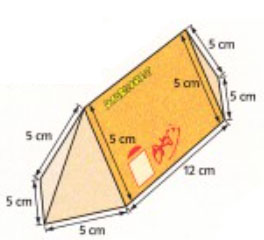
Berechne Volumen und Materialbedarf der Schachtel.

Aufgabe 4:

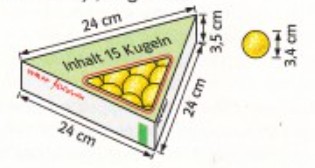
Wie viel Prozent Luft ist in dieser Verpackung? Lassen sich die Schokoladenkugeln Platz sparender anordnen? Wenn ja, zeige wie.

Aufgabe 5:

Betrachte die Verpackung links.

a) Verändere eine Länge so, dass ein Volumen von 1500 cm^{3} ±10 % entsteht. Gib zwei Möglichkeiten an. Welche von beiden ist Material sparender?

b) Zeichne das Körpernetz.

Answer 1

( schwieriger )
1.)
h = 100 cm
d = 80 cm
r = 40 cm
s = Länge Seitenlinie = √ ( r^2 + h^2 )
s = √ ( 40^2 + 100^2 ) = 107.7

V = 1/3 * π * r^2 * h ( Formelsammlung )
O = r * π * ( r + s ) ( Formelsammlung )

V = 1/3 * π * r^2  * h
V = 1/3 * π * 40^2 * 100
V = 167552 cm^3

O = r * π * ( r + s )
O = 40 * π * ( 40 + 107.7 )
O = 18561 cm^2

Der Vergleich mit a.) kann nicht geführt werden da a.) nicht bekannt

2.)
Die Höhe und der Durchmesser der zylindrischen Dose sind gleich.
h = d = 2 * r
V(D) = r^2 * π * h ( Formelsammlung )
V(D) = r^2 * π * 2 * r
V(D) = r^3 * π * 2

Die schraffierte Fläche entspricht einer Halbkugel.
V(K) = 1/3 * π * r^3 ( Formelsammlung )

V(K) zu V(D) = V(K) / V (D) = ( 1/3 * π * r^3 )  / ( r^3 * π * 2  )
V(K) zu V(D) = (1/3 ) / 2 = 1/6 = 0.16666 = 16.6 %

5.)
Die Vorderfront ist ein Rechteck plus ein halber Kreis.
a = 12 cm
h = 9 cm
r = a / 2 = 6 cm

A = a * h + r^2 *π / 2
A = 12 * 9 + 6^2 * π / 2
A = 164.55 cm^2

b = Tiefe = 12 cm

V = A * b = 164.55 * 12
V = 1974.6 cm^3

V = 1500 cm^3 ( gewünscht )
c = neue Tiefe
V = A * c = 164.55 * c = 1500
c = 9.12 cm

Bei einer Tiefe von 9.12 cm ist das Volumen 1500 cm^3.

So. Die anderen Aufgaben sind auch noch viel zu rechnen.
Ich muß erst einmal Schluß machen.

Comments

Zu 4.)
Kugel : von oben betrachtet
r = d/2 = 1.7 cm
V = 4/ 3 * π * r^3 = 20.58 cm^3

gleichseitiges Dreieck
s = 24 cm
s^2 = ( s/2)^2 + h^2
576 = 144 + h^2
h = 20.78 cm
A = s * h / 2
A = 249.4 cm^2
V = A * 3.5 = 872.9 cm^3

15 * 20.58 = 308.7 cm^2

V ( Kugeln ) / V ( Dreieck ) = 308.7 / 872.9 = 0.3536
entspricht 35.36 %
Luft = 100 - 35.36 = 64.64 %

---

Zu 3.)
Es ergibt sich meiner Meinung nach keine eindeutige
Schachtelform.

Frage : habt ihr die 5 Aufgaben als eine Hausaufgabe auf ?
Das ist aber eine Menge Arbeit.

---

Nein, nicht als als eine Hausaufgabe, sondern diese Aufgaben sind eine Vorbereitung für die Arbeit, die ich nächste Woche zu schreiben habe.

---

Wofür stehen die Abkürzungen V(K) und V(D)?

---

Volumen ( Kugel )
Volumen ( Dreieck )

Hier noch die dichteste Packung der Kugeln.
5 - 4- 3- 3- 2 -1

Die Abstände mit du dir wegdenken.

---

Danke für diese ausführlichen Erklärungen! Ich hätte da noch ein paar Frage. 

Zu 5) Um angeben zu können, welche Möglichkeit, von den beiden Möglichkeiten, Material sparender ist, muss ich die Oberfläche herausfinden. Könntest du mir erklären, wie man die Oberfläche herausfindet?

Zu 2) Was meinst du mit Volumen (Dreieck)? Ich sehe überhaupt kein Dreieck und ein Dreieck kann doch kein Volumen haben. Meintest du nicht Volumen (Zylinder)? Und ist für die Formel des Volumens einer Kugel wirklich "1/3 * π * r³?" Denn in meiner Formelsammlung steht bei der Berechnung des Volumens einer Kugel   4*π *r³ /3.

Und falls du kannst, könntest du mir bitte auch Aufgabe 3 erklären?

---

zu 5.)

a = 12 cm
h = 9 cm
A = a * h + (a/2)² *π / 2
b = Tiefe = 12 cm

V = A * b
V =  ( a * h + (a/2)² *π / 2 ) * b

Gesamtfläche O(berfläche)
Umfang Vorderfront
U = a + 2 * h + a * π /2
O = U * b + 2 * A
Beispiel Ausgangsverpackung
A = 164.55
U = 12 +  2 * 9  + 12 * π / 2 = 48.85 cm
O = 2 * 164.55 + 48.85 * 12
O = 917.3 cm^2

a = 12 cm
h = 9 cm
b = 12 cm
Gewünscht V = 1500
V = ( a * h + (a/2)² *π / 2 ) * b
2 Variable so belassen und die 3.ausrechnen
z.B. b = 9.12 cm
Dann die Fläche O berechnen.
Eine 2.Berechnung machen z.B h ist variabel.
Neues h ausrechnen. O ausrechnen und
das Material vergleichen.

zu 2.)
V ( D ) ist Volumen Dose.

Die schraffierte Fläche entspricht einer Halbkugel.
V(K) = 1/3 * π * r³ ( Formelsammlung ) 

Hier muß es heißen

V(K) = 4/3 * π * r³   / 2 ( Formelsammlung  Halbkugel )
V(K) = 2/3 * π * r³ 
V(K) zu V(D) = V(K) / V (D) = ( 2/3 * π * r³ )  / ( r³ * π * 2  )
V(K) zu V(D) = (2/3 ) / 2 = 1/3 = 0.33333 = 33.33 %

zu 3.)
Kann ich leider nicht bzw. nicht über das Internet.
Ich bin der Meinung es ergibt sich keine eindeutige
Schachtelform.

---

Jetzt hab' ich die von dir erklärten Aufgaben verstanden.

---

Du hast die Aufgaben gut mitverfolgt und dadurch ein paar Fehler
gefunden. Die Aufgaben waren aber doch eine ziemliche Rechnerei.

Ich wünsche dir eine gut verlaufende Mathearbeit.

mfg Georg

Answer 2

2s: Halbkugel im Zylinder

3s: Die Enden sind jeweils eine halbe Pyramide

4s: Volumen Schachtelfläche Dreieck mal Höhe vs. Kugelvolumina

Comments

Könntest du auch nachvollziehbare Lösungswege nennen? Also mit Formeln und eventuell mit Erläuterungen. Und meinst du bei 4s, dass man den Flächeninhalt des großen Dreiecks mit der Höhe multiplizieren muss um das Volumen herauszufinden?

---

Ja, Fläche mal Höhe ergibt Volumen.