Ein Deich ist ein Schutzwall gegen das Meer mit einer steilen Böschung zur Landseite und einer flacheren Boschung an der Seeseite, so dass die auflaufenden Wellen ihre \( \mathrm{Kraft} \) verlieren.
Ältere Deiche an der Nordseeküste haben ein Deichprofil, dessen form auf einem bestimmten Deichabschnitt näherungsweise dem Graphen der Funktion \( f_{1} \) entspricht mit
\( f_{1}(x)=\frac{1}{3 t} x(x-3 t)^{2} ; t \geq 1 \)
und einem geeigneten Definitionsbereich. Dabei beschreibt die negative \( x \)-Achse im Koordinatensystem den Veriauf des Lands hinter dem Deich, die positive \( x \)-Achse die Deichsohle und die Meeresoberfläche.
Der abgebildete Graph zeigt das Deichprofil für \( t=2 \).

d) Von der Deichkrone aus soll ein unterirdisch verlaufendes, gerades Entwässerungsrohr bis zum Punkt \( \mathrm{O}(0 \mid 0) \) verlegt werden.
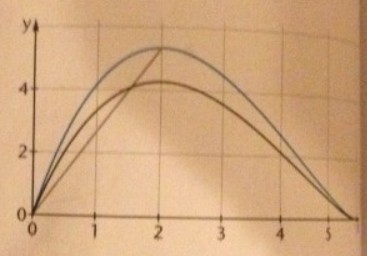
(1) Bestimmen Sie die Länge dieses Rohrs sowie die Länge der Strecke, für die das Rohr innerhalb der Sandschicht verläuft.
(2) Bestimmen Sie die Stelle auf dem Deich, an der der senkrecht zur Meeresoberfläche gemessene Abstand zum Rohr am größten ist.
Ansatz/Problem:
Ich muss die Länge wahrscheinlich mit Pythagoras ausrechnen.