(u^{2}+2i)+4=p(z) und p(z)=z^{5}-2z^{4}+z-2 Nullstellen berechnen

Question

Ich habe vorrallem probleme dann die Lösung zu bestimmen wenn es um den zeichnerischen geht.

Wie zum beispiel z^{2}=-4i

Danke für hilfe^^

Ich hab mal was von komplexeren zahlen gehört

Sowas die hoch komplexe zahlen oder ultra komplrxe zahlen gibt es sowas?

Answer 1

Nullstellen von Polynomen sind immer noch komplexe Zahlen, da brauchst du nichts zu erweitern also keine 'komplexeren Zahlen. In der Zahlenebene zeichnest du komplexe Zahlen z = a+ib genau so, wie du den Punkt P(a,b) in ein xy-Koordinatensystem einzeichnest. Statt mit x und y bezeichnest du die Achsen aber mit "reelle" und "imaginäre Achse." 

  (u²+2i)+4=p(u) . Du meinst sicher p(u). Oder? 

 
und p(z)=z⁵-2z⁴+z-2 Nullstellen berechnen. 

  z⁵-2z⁴+z-2     | (z-2) ausklammern 

 = z^4(z-2) + 1*(z-2) 

 = (z^4 + 1)(z-2) 

 1. Nullstelle z₁ = 2 

 2. bis 5. Nullstelle: die 4 Lösungen von z^4 + 1 = 0

 0 = z^4 + 1 = z^4 - i^2  = (z^2 -i)(z^2 + i) 

 2. und 3. Lösung aus z^2 = i 

 z₂ = 1/√2 ( 1 + i) 

 z₃ = 1/√2 (-1-i) 

 4. und 5. Lösung aus z^2 = -i 

 z₄ = 1/√2 (-1 +i) 

 z₅ = 1/√2 (1 -i) 

 
Nun das Koordinatensystem wie oben beschrieben zeichnen und die berechneten Punkte einzeichnen.

Das sollte dann aussehen wie hier: https://www.wolframalpha.com/input/?i=z%5E5-2z%5E4%2Bz-2

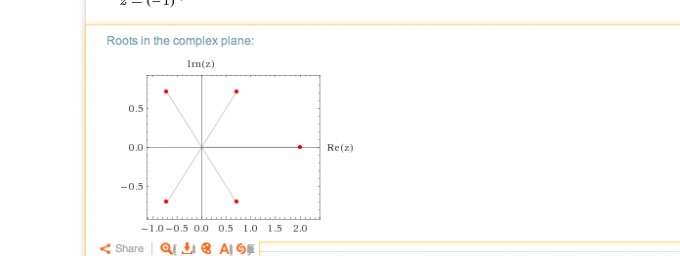
Dadurch, dass hier die reelle und die imaginäre Achse nicht gleich skaliert sind, liegen die 4 komplexen Wurzeln nicht so exakt auf einem Quadrat, wie in deiner Zeichnung.

EDIT: Entschuldige die vielen Leerzeilen oben. Zuerst wurden alle Zeilenumbrüche entfernt. Ich habe sie daher doppelt gesetzt.

Comments

Danke

Ich meinte aber

p(z)= komplexe funktion

z2 = 1/√2 ( 1 + i) 

wie du auf das kammst vetstehe ich nicht.

Vorallem (1+i) part verstehe ich nicht.

Edit: überhaupt kein thema ;) 

---

Bei komplexen Zahlen nennt man alle Lösungen z von z^n = u Wurzeln von u.

Man betrachtet u am besten in Polarform. r ist der Betrag von u und φ der zur Zahl gehörige Winkel.

Lies nun erst mal folgenden Artikel ganz genau durch:

https://de.wikipedia.org/wiki/Wurzel_(Mathematik)#Wurzeln_aus_komplexen_Zahlen

z² = i 

Hier also erst mal die Polarform überlegen: Betrag von i ist 1 und der zugehörige Winkel ist 90° = π/2.

Nachdem du den angegebenen Artikel gelesen hast, weisst du nun, dass z1 und z2 ebenfalls den Betrag 1 haben und ihre Winkel (sog. Argumente) 45° und 180° + 45° = 225° sind.

1+i hat Argument 45° ist aber mit dem Betrag r =√(1+1) = √2 zu lang.

Daher z_(1) = 1/√2 * (1+i)

analog komme ich auf z_(2). Resultate vgl. oben.

"Ich meinte aber

p(z)= komplexe funktion" 

Das z allein sagt noch nicht, dass eine komplexe Funktion vorliegt. Deutet aber darauf hin. p steht eher für "Polynom" und die Variable im Argument der Funktion ist die Variable der Funktion. Sie muss links und rechts vom Gleichheitszeichen gleich heissen. Also nicht 

  (u²+2i)+4=p(z) , wenn du möchtest, dass das u eine Variable ist.

---

die funktion war eine komplexe. ich habe mich lediglich nur verschrieben.

alle buchstaben waren mit einem z versehen^^.

die aufgaben stellung hiess ja löse die komplexe nullstelle.

ich versuche es jetzt noch mal wenn ich es nicht hinbekomme frage ich noch mal nach 

danke

immai

---

Hier also erst mal die Polarform überlegen: Betrag von i ist 1 und der zugehörige Winkel ist 90° = π/2.Nachdem du den angegebenen Artikel gelesen hast, weisst du nun, dass z1 und z2 ebenfalls den Betrag 1 haben 

Bis dahin ist mir alles klar ;)

und ihre Winkel (sog. Argumente) 45° und 180° + 45° = 225° sind.

Den Part verstehe ich nicht.

Ab da fehlt mir der verständniss.

Danke

---

Ein Argument deines z ist: 90° : 2 = 45°, da du die 2. Wurzel willst.

Nun gibt es noch eine zweite Zahl, die quadriert i gibt.

Rechne: 45° + 360°/2 = 225°.

Weitere Argumente wären 45° + k*360°/2 ..... Da kommt nichts mehr Neues dazu zwischen 0° und 360°.

---

Also

z^{2}=i

Hat den betrag 1

Also 90º 

z^{2}=90º?

Und dann warum durch 2 welche beziehung zu der wurzel hat es hier?

---

Ein Argument deines z ist: 90° : 2 = 45°, da du die 2. Wurzel willst.

n.wurzel(|a|)=

Hat das damit zu tun?

Warum wir die 90 durch 3 teilen

Wenn es 3 wurzel wäre dann durch 3?

Und dann noch 

Nun gibt es noch eine zweite Zahl, die quadriert i gibt.Rechne: 45° + 360°/2 = 225°. 

Wie bestimme ich das?

Woher weiss ich das es keine dritte gibt?

Liegt das an der anzahl der wurzel?

---

Das Wesentliche hast du eigentlich erkannt. Aber: n.wurzel(|a|)= r nicht Argument (Winkel)

Ein Kurzversion zur nötigen Theorie findest du im Link, den ich dir angegeben habe. Hier nochmals https://de.wikipedia.org/wiki/Wurzel_(Mathematik)#Wurzeln_aus_komplexen_Zahlen

Da steht alles Wichtige drinn. 

Ausführlichere Begründungen sollten in jedem Skript / Lehrbuch zu komplexen Zahlen stehen.

---

Anmerkungen direkt in deinen Kommentaren:

" z²=i

Hat den betrag 1

und das Argument 90º 

arg(z²)=90º?

Und dann warum durch 2 welche beziehung zu der wurzel hat es hier? vgl. Kommentar oben.

 Kommentiert vor 3 Stunden von immai  

Ein Argument deines z ist: 90° : 2 = 45°, da du die 2. Wurzel willst.

n.wurzel(|a|)=r

Hat das damit zu tun?

Wenn wir die 90 durch 3 teilen

 ist es das Argument der 3 wurzel .

Und dann noch 

Nun gibt es noch eine zweite Zahl, die quadriert i gibt.Rechne: 45° + 360°/2 = 225°. 

Berechne mal 45° + 2* 360° / 2 und überlege, wie du das in der komplexen Zahlenebene eintragen könntest.

---

1+i hat Argument 45° ist aber mit dem Betrag r =√(1+1) = √2 zu lang.

r=w(1+1)

Woher kommen die 1er?

Wegen 1+i(=1?)

Danke für deine muehen bis jetzt.

Versuche grad 45+360=405 zu berechnen

Dafuer muss ich ja aber zuerat das mit 1+i verstehen

---

Also r setzt sich durch r=w(a^2+b^2)

Das ist mir eingefallen und aufgefallen.

Wie setzt sich jetzt aber 

405º ein?

Wie kann ich die 360 grad mit einebziehen?

---

Ah jetzt verstehe ich auch die 225º

Also

r=w(-1^2-i^2)=w(2)

1/w(2)×(-1-i)

Ist das so korrekt?

Aber das mit 405 wuesste trotzdem nicht weiter

---

Lu bist du da? ;)        

---

Ich möchte, dass du endlich mal dein Skript (oder ein Lehrbuch) rausnimmst. Es hat keinen Sinn, dir die ganzen komplexen Zahlen zu erklären, bei einer Kontrollaufgabe zu dieser Theorie.

Zu den Winkeln: Geh hier (Bild aus https://de.wikipedia.org/wiki/Polarkoordinaten ) mal zum Winkel 405°. Gibt es einen Unterschied zum Winkel 45°? (Hoffentlich nicht!)