Wie bestimmt man den Winkel zwischen zwei Vektoren?

Question

Ich muss herleiten, wie man den Winkel zwischen zwei Vektoren in der Ebene (zweidimensional) bestimmt.

Kann mir jemand bitte eine verständliche Schritt-für-Schritt-Anleitung aufzeigen?

Als Beispiel-Vektoren seien gegeben:

$$\vec{ x_1 } = \begin{pmatrix} 1\\1 \end{pmatrix}$$

$$\vec{ x_2 } = \begin{pmatrix} 2\\3 \end{pmatrix}$$

Vielen Dank :)

Answer 1

Benutze das Skalarprodukt.

Es gilt u * v = |u| * |v| * cos φ.

(u * v) / ( |u| * |v| ) = cos φ

u * v = (1,1) * (2,3) = 1*2 + 1*3 = 5

|u| * |v| = √(1+1) * √(4+9) = √2 * √13 = √26

cos φ = 5/√26

φ = 11.31°

Comments

Könntest du mir bitte die Formel erklären. Also was bedeutet jedes einzelne Element?

---

Ich benutzte u und v statt x1 und x2.

Lies nun das hier https://de.wikipedia.org/wiki/Skalarprodukt

ganz genau durch. Sonst kannst du das Vorgerechnete gar nicht verstehen.

---

Hallo ,

ich habe noch nicht ganz verstanden, wie man bei der Formel cos(phi)= (u*v) / (IuI*IvI)  auf den Betrag kommt.

Liebe Grüße

---

Das musst du nicht verstehen. Das ist die Definition des Skalarprodukts, die ich dir oben verlinkt habe.

---

ich muss es leider in einer gfs meinen Mitschülern erklären...

---

Welches Thema bekandelt ihr denn gerade? Welche Klasse? Das ist eine typische Aufgabe aus der Vektorgeometrie. Da sollten alle das Skalarprodukt schon kennen.

Wenn ihr erst Geradengleichungen y = mx  + q behandelt habt, machst du es besser damit.

Answer 2

Hi,

arbeite auf Grundlage von

a * b = |a| * |b| * cos(φ)

Dabei ergibt sich a*b geometrisch betrachtet aus dem Vektor a, welcher auf b projeziert wird. Bzw. dessen Länge, welche durch |a|*cos(φ) und |b| sich ergibt.

Dann eben obiges nach φ auflösen.

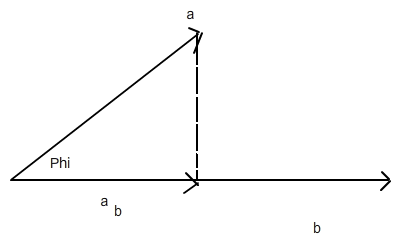
wobei a_(b) der projezierte Vektor mit der Länge |a|cos(φ) ist.

Grüße