Aufgabe:
Ein Mast soll mit 20 m langen Seilen abgesichert werden.
- Bestimmen Sie die Höhe, in der diese Seile am Mast angebracht werden müssen, wenn ihr Neigungswinkel 65° sein soll.
- Fertigen Sie eine Skizze an.
- Berechnen Sie die Entfernung zum Mast, in der die Seile am Boden befestigt werden müssen.
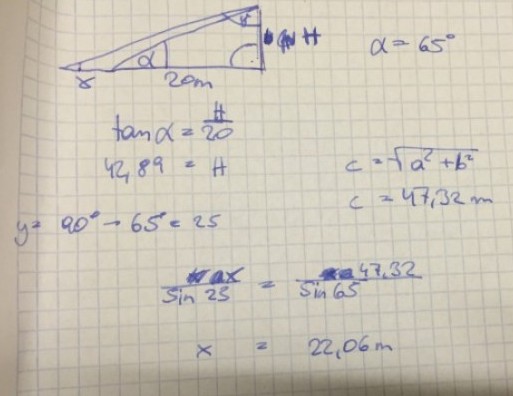
Ansatz/Problem:
Bitte meine Lösung kontrollieren: