Aufgabe:
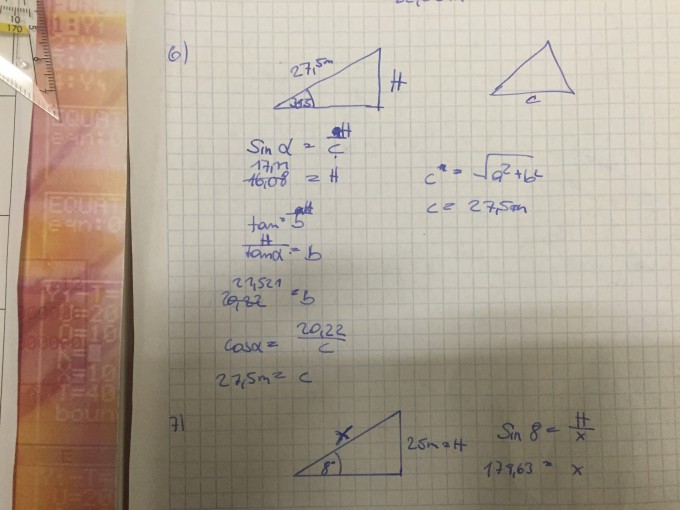
6. Bestimmen Sie die Höhe einer Tanne, wenn ihr Schatten \( 27,5 \mathrm{~m} \) lang ist und die Sonnenstrahlen unter dem Winkel \( 38,5^{\circ} \) einfallen.
7. Beantworten Sie folgende Frage mit einer nachvollziehbaren Berechnung: „Wie weit fliegt ein Drachenflieger, der in \( 25 \mathrm{~m} \) Höhe unter einem Gleitwinkel von \( 8^{\circ} \) startet?“ Untermauern Sie ihre Gedankengänge mit einer Skizze.
8. Von der Spitze eines \( 28,6 \mathrm{~m} \) hohen Turms erscheint die Breite des \( 6 \mathrm{~m} \) entfernten Flusses unter einen Sehwinkel von \( 17^{\circ} \).
- Fertigen Sie eine Skizze an.
- Berechnen Sie die Breite des Flusses.
9. Für einen \( 12 \mathrm{~m} \) entfernten Beobachter mit der Augenhöhe \( 1,6 \mathrm{~m} \) erscheint der Fahnenmast auf der Spitze eines \( 15 \mathrm{~m} \) hohen Turmes unter dem Sehwinkel von \( 6,5^{\circ} \).
- Fertigen Sie eine Skizze an.
- Bestimmen Sie die Lnge des Fahnenmastes.
Ansatz/Problem:
Bitte meine Lösung kontrollieren: