Rein mathematisch
Schnittpunkte der Funktion mit der x - Achse : y = 0
f ( x ) = -a * ( x² -1 )
-a * ( x² -1 ) = 0
Ein Produkt ist dann 0 wenn mindestens 1 der Faktoren 0 ist.
x^2 - 1 = 0
x^2 = 1
x = + 1
x = - 1
N ( - 1 | 0 )
N ( + 1 | 0 )
Stammfunktion bilden
f ( x ) = -a * ( x² -1 )
s ( x ) = -a* ( x^3 /3 - x )
Integralfunktion
[ -a * ( x^3 /3 - x ) ]
-11-a vorziehen
-a * [ x^3 /3 - x ]
-11-a * [1^3/ 3 - 1 - ( (-1)^3 / 3 - (- 1) ) ]
-a * [ 1/3 - 1 + 1/3 - 1 ]
-a * ( - 4 /3 )
4 / 3 a
Soll 2 sein
4 / 3 * a = 2
a = 3 / 2
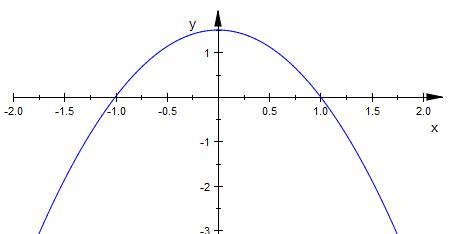
Der Vollständigkeit halber sei erwähnt das eine Lösung
a = - 3 / 2 die Parabel noch oben umdrehen würde und
die Fläche ( absolut ) dieselbe wäre.
Es gibt also 2 Lösungen.
mfg Georg