für die Funktionsgleichung hast du schon alle relevanten Informationen. Du kannst die Parabel direkt auf die Y-Achse legen, damit sie symmetrisch in der Mitte geteilt wird. Das musst du ja nicht, aber es macht die Rechnerei doch einfacher.
Der Scheitelpunkt deiner Parabel soll also bei (0, 36) liegen, weil die Bogenhöhe 36m ist.
Sie ist unten 72m breit, soll also auf von beiden Seiten der Y-Achse 36m weit aufgespannt sein. Das heißt, deine Parabel schneidet die x-Achse bei x= -36 und x= 36. Das gibt dir insgesamt die Breite von 72m.
Jetzt musst du nur noch die Gleichung aufbauen. Die Gleichungsform einer Parabel (einer ganzrationalen Funktion 2. Grades) lautet im allgemeinen:
$$ y=ax^2+b $$
a: Stauchung/Streckung
b: y-Achsenschnittstelle
Die Stauchung bzw. Streckung sagt deiner Parabel, wie weit sie sich von der Y-Achse aufspannen soll. Du willst, dass sie sich hier 36m auf jeder Seite von ihr aufspannt, also ist die Streckung
$$ a=\frac { 1 }{ 36 } $$
Zudem soll die Parabel sich nach unten hin öffnen. Sie braucht daher ein negatives Vorzeichen vor der Streckung:
$$ y=-\frac { 1 }{ 36 }x^2+b $$
Weil du deine Parabel zentral auf die Y-Achse gelegt hast, ist die Y-Achsenschnittstelle (0,36) gleichzeitig Scheitelpunkt. Das heißt b=36. Die Gleichung lautet also:
$$ y=-\frac { 1 }{ 36 }x^2+36 $$
Sie sieht dann so aus:
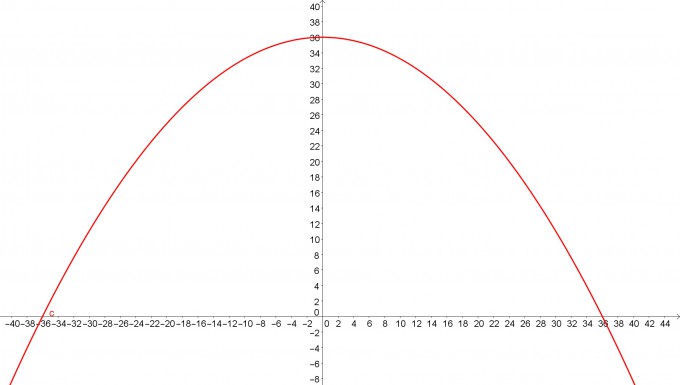
Um jetzt die geforderten Angaben zu bekommen, musst du die jeweils gegebene Höhe oder Breite als Bestandteil deiner Gleichung benutzen.
Um die Breite des Gebäudes bei y=12,7m zu bekommen, rechnest du:
$$ 12,7=-\frac { 1 }{ 36 }x^2+36 $$
und bekommst
$$ x=28,96 $$
Dies ist aber nur für eine Seite. Weil es um die Breite des ganzen Bogens in dieser Höhe geht, musst du dein Ergebnis verdoppeln:
Breite bei y=12,7m: 2(28,96m) = 57,92m
Für die Höhe bei einer Breite von 46,1m ist es das gleiche Spiel: Setze in die Gleichung ein und löse. Aber hier musst du bedenken, dass die angegebene Breite sich auf beide Hälften der Parabel bezieht. Der x-Wert der entsprechenden Höhe y ist also schon verdoppelt worden, genauso wie wir das eben selbst gemacht haben, um die Breite bei y = 12,7m anzugeben. Wenn du nun die hier angegebene Breite in die Gleichung setzt, musst du sie deshalb halbieren:
$$ y=-\frac { 1 }{ 36 }\cdot (\frac { 46,1 }{ 2 })^2+36 $$
Damit bekommst du y = 21,24. Bei einer Höhe von 21,24m ist das Gebäude also 46,1m breit.
Hier eine Zusammenfassung
Gleichung
$$ y=-\frac { 1 }{ 36 }x^2+36 $$
Breite des 3. Stockes bei y=12,7m
57,92 m
Höhe des 5. Stockwerks mit 2x=46,1m Breite
21,24 m
Ich hoffe, ich konnte dir helfen!