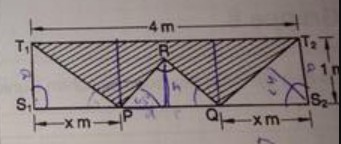
Ein Rechteck \( \mathrm{S}_{1} \mathrm{~S}_{2} \mathrm{~T}_{2} \mathrm{~T}_{1} \) hat die Seitenlängen \( \mathrm{S}_{1} \mathrm{~S}_{2}=4 \mathrm{~m} \) und \( \mathrm{S}_{1} \mathrm{~T}_{1}=1 \mathrm{~m} \).
Auf \( \mathrm{S}_{1} \mathrm{~S}_{2} \) werden \( \mathrm{P} \) und \( \mathrm{Q} \) mit \( \mathrm{S}_{1} \mathrm{P}=\mathrm{QS}_{2} \) \( =x ~ m \) (Meter) so verschoben, dass das Dreieck PQR stets gleichschenklig, rechtwinklig ist. Die schraffierte Fläche habe den Flächeninhalt \( \mathrm{A} ~ \mathrm{m}^{2} \).
Welche Funktion ordnet der möglichen Zahl \( x \) die Inhaltszahl A zu? Für welches \( x \) ist \( \mathrm{A} \) maximal? Welches ist der größte Inhalt?