Die Lösung ist auch mit dem Sinussatz möglich:
$$ \frac { a }{ \sin { (\alpha ) } } \quad =\quad \frac { b }{ \sin { (\beta ) } } \quad =\quad \frac { c }{ \sin { (\gamma ) } } $$
Für deine Werte (Seite AB = c = 10 cm, Seite BC = a = 5 cm und Winkel α = 21°):
$$ \frac { 5cm }{ \sin { (21°) } } \quad =\quad \frac { 10cm }{ \sin { (\gamma ) } } \quad \quad |\quad Kehrwert\\ \\ \frac { \sin { (21°) } }{ 5cm } \quad =\quad \frac { \sin { (\gamma ) } }{ 10cm } \quad \quad |·10cm\\ \\ \frac { \sin { (21°) } }{ 5cm } \quad ·10cm\quad =\quad \sin { (\gamma ) } \\ \\ \sin { (\gamma ) } \quad =\quad 0,71673589909060055\quad \quad |\sin ^{ -1 }{ () } \\ \\ \gamma \quad =\quad \sin ^{ -1 }{ (0,71673589909060055) } \\ \\ \gamma \quad \approx \quad 45,786° $$
Und wie Julian schon geschrieben hat, gibt es ein zweites mögliches Ergebnis, da der Sinuswert von sin(45,786°) ≈ 0,7167 sowie der Sinuswert von sin(180° - 45,786°) = sin(134,214°) ≈ 0,7167 ist. Siehe Identitäten.
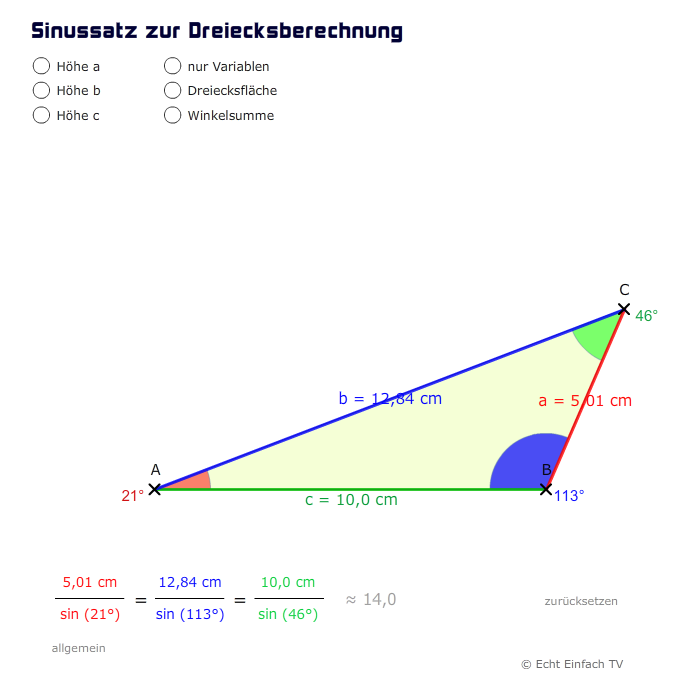
PS: In der Lektion Sinus und Kosinus bei Allgemeinen Dreiecken (Sinussatz) findest du das Programm "Sinussatz zur Dreiecksberechnung". Dort kannst du deine Werte eingeben und die Lösung wird berechnet: