Kreis: Suche Gleichung der Tangenten, die normal g:X=(2l-5)+t*(1l4) sind.

Question

Ermittle die Gleichungen der Tangenten an den Kreis k, die normal zur Geraden g sind, und gib die Koordinaten der Berührungspunkte an !

k: (x+3)²+(y-3)²=68, g:X=(2l-5)+t*(1l4)

formel: r²*(k²+1)=(k*X_M-Y_M+d)²

bitte mit Rechenschritte

danke!

Answer 1

Der Mittelpunkt des Kreises ist M(-3 | 3).

Ich nehme jetzt eine Parallele zu g die durch M geht

x = X=(-3 l 3) + t*(1 l 4) = (t-3 | 4t+3)

Und bilde hier den Schnittpunkt mit dem Kreis. Also setzte ich es in die Kreisgleichung ein:

(x + 3)^2 + (y - 3)^2 = 68
((t-3) + 3)^2 + ((4t+3) - 3)^2 = 68
(t^2 + ((4t)^2 = 68
17t^2 = 68
t = ±2

Damit sind die Tangentenpunkte

(t-3 | 4t+3) = (2-3 | 4*2+3) = (-1 | 11)

(t-3 | 4t+3) = ((-2)-3 | 4*(-2)+3) = (-5 | -5)

Nun brauche ich noch einen Richtungsvektor Senkrecht zur Geraden g. Das ist aber nicht wild. Ich vertausche x und y Koordiate und drehe eins davon noch im Vorzeichen um.

(1 l 4) --> (4 | -1)

Damit lauten die Tangentengleichungen:

(-1 | 11) + r * (4 | -1) und (-5 | -5) + r * (4 | -1)

Comments

@Mathecoach: Machst du auch nichts mit der angegebenen Formel? Habe die bei einer andern(?) gerade kommentiert.

---

Mir sagt die Formel auch so nichts

r²*(k²+1)=(k*X_M-Y_M+d)²

^{r dürfte wohl für den Radius stehen. XM und YM für den Kreismittelpunkt und k irgendeine Konstante. Aber für eine Tangentengleichung würde ich doch in irgendeiner Form eine Geradengleichung vermuten. Und die kann ich nicht wirklich in dieser Formel erkennen. Also ich kann die Formel momentan leider nicht einordnen.}

---

r²*(k²+1)=(k*X_M-Y_M+d)²funktioniert das auch hier nicht mit dieser Formel

---

vgl. :

https://www.mathelounge.de/20186/gleichung-der-tangenten-den-kreis-die-parallel-3x-verlauft?show=20233#c20233

k anscheinend Tangentensteigung und d y-Achsenabschnitt der Tangente. Ist allerdings unklar.

---

g: X = (2 l -5) + t*(1 l 4)

Die Steigung ist hier der Richtungsvektor und damit 4/1 = 4. Die Steigung der Tangente muss der negative Kehrwert also k = -1/4 sein.

Mit der Formel ergibt sich

((- 1/4)·(-3) + d - 3)^2 = √68^2·((- 1/4)^2 + 1)
d = 10.75 ∨ d = -6.25

Damit lauten die Tangenten

y1 = -1/4x + 10.75

y2 = -1/4x - 6.26

Eigentlich finde ich es dann unsinnig dies noch in die Koordinatenform umzuwandeln. Das würde dann wie folgt gehen:

 

y = -1/4x + 10.75
4y = -x + 43
x + 4y = 43

Answer 2

k: (x+3)^2+(y-3)^2=68, g:X=(2l-5)+t*(1l4)

formel: r^2*(k^2+1)=(k*XM-YM+d)^2

g:X=(2l-5)+t*(1l4)

Steigung von g: 4/1

Steigung der Tangente: -1/4

Versuch mit deiner Formel:

68 (1/16 + 1) = (-1/4 * (-3) + 3 + d)^2

72.25 = (3.75 + d)^2      |√

±8.5 = 3.75 + d

-3.75 ± 8.5 = d

d1 = 4.75            

 t1: y = -1/4 x + 4.75       resp.

t1: x + 4y = 19 

d2 = 12.25

t2: y = -1/4 x + 12.25

t2: x + 4y = 49

Comments

1) da fehlen noch zwei Punkte t₁:4x-y=-49 , T₁(-11/5), t₂: 4x-y=19, T₂(5/1) (Lösungsheft)

2) t1: x + 4y = 19

    t2: x + 4y = 49

sind diese Ergebnisse richtig wie von der Lösungsheft

---

Setze jeweils x und y der Punkte in die Geraden und in die Kreisgleichung ein. Wenn's stimmt, hat das Lösungsweg recht.

(-1|11) hat Mathecoach auch. Mach zB mal eine Skizze.

Wie man's rechnen kann, hab ich gerade bei der andern Aufgabe geschrieben.

Answer 3

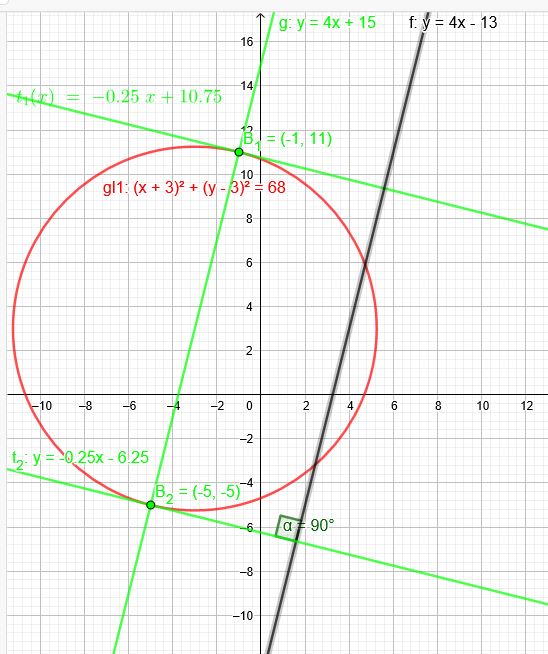
Ermittle die Gleichungen der Tangenten an den Kreis k, die normal zur Geraden g sind, und gib die Koordinaten der Berührungspunkte an !

\(k: (x+3)^2+(y-3)^2=68\),     g:X=(2l-5)+t*(1l4)

Parameterform  in die Koordinatenform umwandeln

\(x=2+1t\)   → \(t=x-2\)

\(y=-5+4t\)   →  \(y=-5+4(x-2)=4x-13\)   mit \(m=4\)

Normalensteigung: \(m_N=-\red{\frac{1}{4}}\)

\(f(x,y)= (x+3)^2+(y-3)^2-68\)

Ableitung nach x:

\(f_x(x,y)= 2(x+3)\)

Ableitung nach y:

\(f_y(x,y)=2(y-3)\)

Allgemeine Form:

\(f'(x)=-\frac{f_x(x,y)}{f_y(x,y)}\)

\(f'(x)=-\red{\frac{1}{4}}\)

\(-\red{\frac{1}{4}}=-\frac{2(x+3)}{2(y-3)}\)

\(\frac{1}{4}=\frac{(x+3)}{(y-3)}\)

\(y=4x+15\) Diese Gerade schneidet den Kreis in den beiden Berührpunkten \(B_1( -1|11)  \) und \(B_2( -5|-5)  \)

1.Tangente :

\( \frac{y-11}{x+1}=-\red{\frac{1}{4}} \)

\( y=-\frac{1}{4}(x+1)+11=-0,25x+10,75\)

Analog die 2.Tangente berechnen.