Viele mathematische Probleme sind nicht analytisch lösbar. Das heißt soviel wie: man kann sie nicht mit Stift und Papier lösen, weil im Rahmen der "gewöhnlichen" Mathematik einfach keine mathematisch exakten Ausdrücke für die Lösungen existieren.
Wenn das der Fall ist (und das ist wie gesagt relativ häufig) dann überlässt man die Arbeit häufig einem Computer, indem man die Aufgabe in einer geeigneten Art und Weise aufbereitet und sich schließlich mit einem Ergebnis einer gewissen Fehlertoleranz zufrieden gibt.
Wenn man nun ein solches Programm schreibt, dann benötigt es gewisse Grundeingaben vom Benutzer, um anfangen zu können.
Ein einfaches Beispiel ist die Lösung der transzendenten Gleichung
5*(e-x - 1) = x
Dass eine Lösung existiert sieht man recht einfach, wenn man linke und rechte Seite als Funktionsgleichung interpretiert - dann entspricht die Lösung nämlich der Schnittstelle der Graphen:
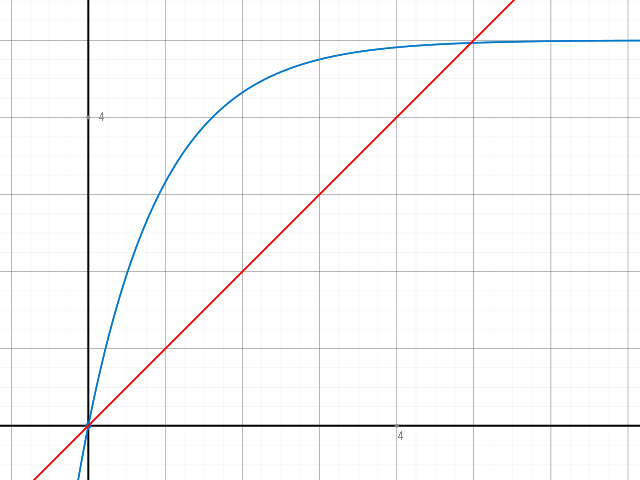
Wir sind hier an der zweiten Lösung interessiert, die erste (x=0) ist relativ einfach zu ermitteln.
Hierfür gibt es ein Lösungsverfahren, dass die Lösung iterativ berechnet, also durch wiederholtes Anwenden einer gewissen Funktionsvorschrift.
Bei sogenannten kontraktiven Funktionen (und die linke Seite stellt eine solche Funktion dar) kann der Fixpunkt, also die Stelle x, für die f(x) = x gilt, einfach durch wiederholtes Anwenden der Funktion ermittelt werden. Indem man also die Folgenglieder berechnet, die sich gemäß
xi+1 = 5*(1 - exi)
ergeben, erhält man aus einem geeigneten Anfangswert eine Folge, die gegen die Lösung konvergiert.
Die Grundeingabe ist nun dieser Anfangswert, denn sie muss noch zusätzlich getätigt werden, wenn der Algorithmus bereits programmiert ist.
(Wählt man z.B. den Anfangswert 5, so ändert sich der Folgenwert bereits nach 3 Anwendungen in der dritten Kommastelle nicht mehr und lautet x ≈ 4,965)