Bestimme die Funktionsgleichung für die Stollenlänge rechnerisch und zeichnerisch

Question

Im Bergbau soll ein alter Stollen weiter ausgebaut werden. Ein Mitarbeiter hat für diesen Stollen folgenden Zeitplan aufgestellt, an dem abgelesen werden kann wie lang der Stollen nach jedem Tag sein muss.

Tage	1	2	3	4	5	6	7	8
Län.Stollens (in m)	13	16	19	22	25	28	31	34

a)Bestimme die Funktionsgleichung rechnerisch, die den Zusammenhang Anzahl der Tage->Länge des Stollens (in m) beschreibt (Zwischenergebnis: f₁(x)=3x+10

b) Berechne die Länge des Stollens nach 11 Tagen

d) Mit einem neueren Maschinenmodell könnten die Arbeiter 1,5-mal schneller arbeiten. Allerdings ist dieses Modell für den alten Stollen zu groß, wodurch ein komplett neuer Stollen ausgebaut werden müsste. Begründe, dass die Arbeit mit der neuen Maschine durch die Funktionsgleichung f₂(x)=4,5x beschdrieben werden kann.

e) Ab welcher Stollenlänge würde sich lohnen die neue Maschine einzusetzen? Begründe rechnerisch und zeichnerisch.

Answer 1

Hi,

a) Bestimme die Funktionsgleichung rechnerisch, die den Zusammenhang Anzahl der Tage->Länge des Stollens (in m) beschreibt (Zwischenergebnis: f₁(x)=3x+10)

Schauen wir uns Tag 1 und Tag 2 an. Da haben wir eine Differenz von 3. Das gilt auch für die weiteren Tage. Das deutet also daraufhin, dass pro Tag 3m gegraben werden.

Am Tag 0 (Als Tag1-3) haben wir eine Länge von 10. Das ist also unser Startwert. Es folgt

f(x)=3x+10

 

b) Berechne die Länge des Stollens nach 11 Tagen

x ist die Anzahl der Tage: f(11)=3*11+10=33+10=43

Der Stollen ist nach 11 Tagen 43m lang.

 

d) Mit einem neueren Maschinenmodell könnten die Arbeiter 1,5-mal schneller arbeiten. Allerdings ist dieses Modell für den alten Stollen zu groß, wodurch ein komplett neuer Stollen ausgebaut werden müsste. Begründe, dass die Arbeit mit der neuen Maschine durch die Funktionsgleichung f₂(x)=4,5x beschdrieben werden kann.

Es muss komplett neu gestartet werden -> Wir haben keinen Startwert (bzw. dieser ist 0). Wir sind außerdem 1,5-mal schneller. Statt 3m am Tag, also 1,5*3m am Tag -> 4,5m am Tag.

Demnach f(x)=4,5x

e) Ab welcher Stollenlänge würde sich lohnen die neue Maschine einzusetzen? Begründe rechnerisch und zeichnerisch.

Gleichsetzen um rauszufinden, wann beide gleichschnell wären:

3x+10=4,5x    |-3x

10=1,5x           |:1,5

x=20/3

Nach knapp 7 Tagen haben beide Tunnel die gleiche Länge. Wenn der Bau also eine Länge von 4,5*20/3=30m hat, lohnt sich der Einsatz der neuen Maschine.

 

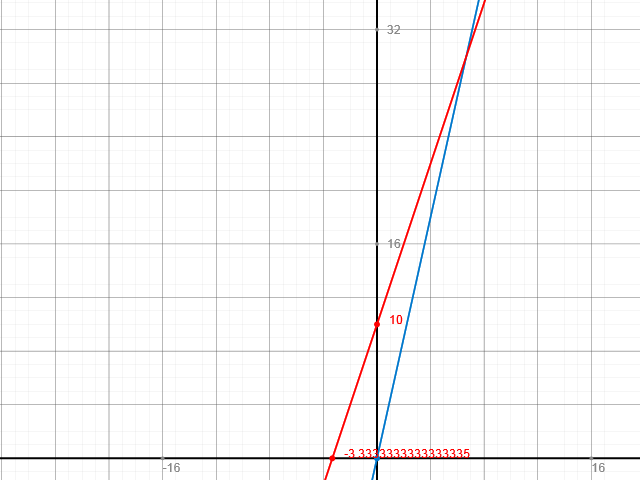
Das wird auch zeichnerisch bestätigt.

 

Grüße

 

 

 

Comments

Rechnung ist prima und richtig. An dieser Stelle nur noch mal eine etwas schönere Zeichnung.

---

Komme mit dem Zeichenprogramm nicht ganz so zu Rande *hust*.

Danke Dir ;).

---

Wobei hast du denn da Probleme?

---

Was das richtige Ausschneiden der interessanten Bereichs angeht.

Entweder ich vernachlässige dann die Achsen, um den Schnittpunkt herauszuzoomen, oder es wird etwas  undeutlich wie oben. Denn ich kann den Bereich nur durch das gegebene "Speicher"-Fenster und Scrollen einschränken?

---

Ach so. Du meinst das Zeichenprogramm dieser Webseite. Ja. Das gefällt mir persönlich auch nicht so gut, weshalb ich lieber auf ein anderes Programm ausweiche. Dort hat man deutlich mehr Möglichkeiten, das genau so anzupassen wie man es haben will.

---

Yup, spreche von dem integrierten Zeichenprogramm, da ich kein eigenes habe. Zeichnen muss ich selbst schon lange nicht mehr^^. Welches nimmst Du denn? Frei erhältlich?

---

Ich benutze http://mathegrafix.de

Die Software ist frei erhältlich. Ich selber habe mir die Lizenz für die Pro Version für 20 Euro gegönnt, damit ich einige Dinge mehr benutzen kann.

Für die meisten Zwecke langt aber auch die normale kostenfreie Version.

---

Man kann Ausschnitte, die man aus den hier erzeugten Graphen, abspeichert, nachträglich noch mit ins Graftiti-Zeichen-Programm von gmf laden und dort von Hand beschriften. Das mach ich aber nur, wenn's wirklich absolut nötig ist.

---

Ok danke euch. Schaus mir heut Mittag mal an.

Jetzt noch letzte Vorbereitungen für Prüfung treffen ;/.

 

Grüße