Differenzenquotienten: Gegeben ist die Funktion f(x)= x^4 - 5x^2 + 4. Gesucht zudem Tangentengleichung.

Question

Die Aufgabe ist. : Bestimme mit Hilfe des Differenzenquotienten die Ableitung an der Stelle x0 = 3.

Die Aufgabe 2 ist. : Bestimme die Gleichung der Tangente an der Stelle x0 = -0.5

BITTE MIT RECHNUNGSSCHRITTEN UND ERKLÄRUNG :)

Answer 1

Ich beginne mit der Tangentengleichung.

f(x)= x⁴ - 5x² + 4

f ' (x) = 4x^3 - 10x

f '(-0.5) = 4*(-0.5)^3 - 10*(-0.5)

         = - 0.5 + 5 = 4.5

f(-0.5) = 0.5^4 - 5*0.5^2 + 4 = 2.8125

t: y = 4.5 x + q

2.8125 = 4.5 * (-0.5) + q

2.8125 + 2.25 = q = 5.0625

t: y = 4.5 x + 5.0625

Skizze als Kontrolle: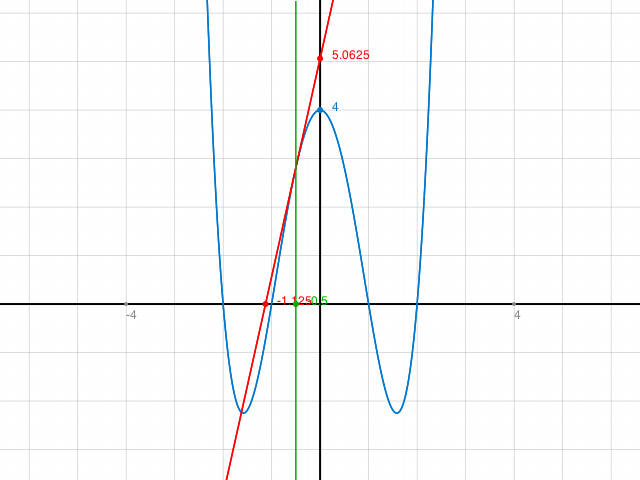

Skizze zum ersten Teil. Hier musste ich den Graphen stauchen. Die Skala auf der y-Achse sollte an den Stellen 4, 40 und 80 beschriftet sein (nicht 0.4, 4 und 8)

Man soll hier gemäss Fragestellung die Steigung im Punkt (3|40) berechnen.

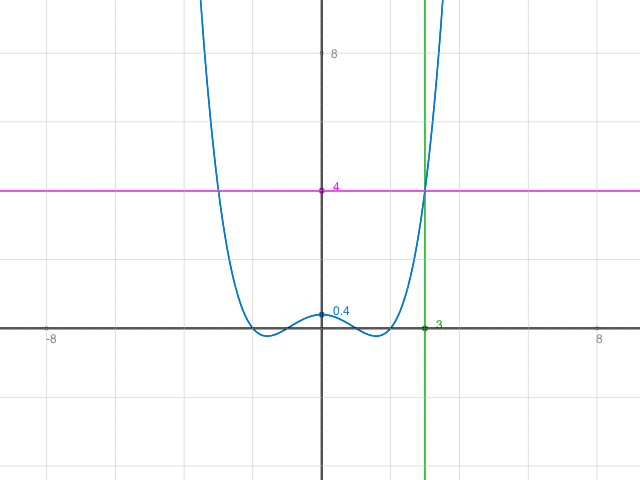
f(x)= x⁴ - 5x² + 4

Ich hoffe jetzt mal, dass du die Regel zum ableiten von Potenzfunktionen schon benutzen darfst.

f ' (x) = 4x^3 - 10x

f ' (3) = 78

Die gesuchte Steigung beträgt 78.

Comments

Bitte. Das Resultat mit der 93 vermutlich schon. Unklar ist nur, ob ihr das so machen dürft. Ist jetzt 78. vgl. Julian.

---

Das Resultat 93 ist für die erste Aufgabe nicht richtig, denn die Ableitung beträgt

f'(x) = 4x^3 - 10x

also

f'(x) = 78

 

Die ausführliche Rechnung mit Differenzenquotient habe ich oben nochmal gepostet.

Answer 2

Da es explizit gewünscht ist, nochmal mit Differenzenquotient:

$$ f ^ { \prime } ( x ) = \lim _ { h \rightarrow 0 } \frac { f ( x + h ) - f ( x ) } { h } $$

Dafür setzt man nun die Funktionsgleichung für den Punkt x ein (ich lasse den Limes erstmal weg und führe den Grenzwert erst ganz am Ende durch):

$$ \begin{array} { l } { \frac { ( 3 + h ) ^ { 4 } - 5 * ( 3 + h ) ^ { 2 } + 4 - \left( 3 ^ { 4 } - 5 * 3 ^ { 2 } + 4 \right) } { h } = \frac { \left( 9 + 6 h + h ^ { 2 } \right) ^ { 2 } - 5 * \left( 9 + 6 h + h ^ { 2 } \right) - 81 + 45 } { h } } \\ { = \frac { 81 + 108 h + 54 h ^ { 2 } + 12 h ^ { 3 } + h ^ { 4 } - 30 h + 5 h ^ { 2 } - 81 } { h } } \\ { = \frac { 78 h + 59 h ^ { 2 } + 12 h ^ { 3 } + h ^ { 4 } } { h } = 78 + h \left( 59 + 12 h + h ^ { 2 } \right) } \end{array} $$

Führt man nun den Grenzwert durch, so geht der zweite Term gegen 0 und übrig bleibt

f'(3) = 78