Fläche I: du brauchst f(x) =-0,5x^2 + 0,5
da du die Fläche zwischen dem Graphen und der x- Achse berechnen musst, musst du zuerst die Nullstellen berechnen -->'
f(x) =0
0 = -0,5x^2+0,5 |-0,5
-0,5 = -0,5x^2 |.(-0,5)
1 = x^2 | wurzel
x1 = 1 x2 = -1
nun hast du den Intervall, also kannst du die Funktion integrieren, am besten jeden einzelnen Term
--> -0,5x^2 = -1/6x^3 0,5 = 0,5x
somit hast du jetzt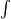 
-0,5x^2 + 0,5 dx = [-1/6x^3 + 0,5x] im Intervall -1 und 1 --> d.h. du setzt 1 und danach -1 in die integrierte Funktion ein und kommst dann auf 1/3 und -1/3 diese subtrahierst du voneinander und kommst auf 2/3 = A1
das gleiche machst du mit b)
Fläche II: du nimmst die f(x) = -0,5x^2+0,5 und g(x) = -1,5 --> die setzt du gleich und berechnest die Schnittpunkte
-0,5x^2 + 0,5 = -1,5 | -0,5
-0,5x^2 = -2 |/(-0,5)
x^2 = 4 | wurzel
x1 = 2 x2 = -2 --> diese beiden nimmst du als Intervall
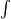(-0,5x^2+0,5)-(-1,5) dx = [-1/6x^3 +2x] und setzt wieder den Intervall ein und kommst auf 2/2/3 und -2/2/3 und subtrahierst sie wieder und kommst auf A2= 5/1/3
das gleiche auch bei b)
Fläche III: du nimmst f(x)= -0,5x^2+0,5
da du schon die Nullstellen berechnet hast und du im 1. Quadranten die Fläche berechnen sollst nimmst du die positive Nullstelle (also x1=1) und 0
die integrierte Funktion hast du schon also brauchst du nur noch 0 und 1 in diese Gleichung einsetzen
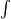-0,5x^2+0,5 dx = [-1/6x^3 + 0,5x] --> 1/3 - 0 = 1/3 = A3
das Gleiche auch in b)
Fläche IV: f(x)= -0,5x^2+0,5
der Intervall ist schon gegeben, da in der Aufgabe steht das die Fläche von -2 und f(x) begrenzt wird im 3. Quadranten... Diesmal nimmst du also die negative Nullstelle (also x2=-1), d.h. du setzt -2 und -1 in die integrierte Gleichung ein
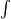-0,5x^2+0,5 dx = [-1/6x^3 + 0,5x] --> 1/3 - (-1/3) = 2/3 = A4
das gleiche mit b)
