Tangente bei einer Kurvenschar fa(x)= a * x^(1/2) - x

Question

Aufgabe:

Gegeben ist die Kurvenschar fa(x)= a * x^(1/2) - x

a>0

a) Bestimmen Sie die Gleichung der Tangente an den Graphen von fa in der positiven Nullstelle. Für welche Wert von a schneidet diese Tangente die Y-Achse im Punkt (0|3)?

b) Der Graph von fa schließt mit der x-Achse im 1. Quadranten ein Flächenstück ein.

Berechnen Sie dessen Inhalt. Für welchen Wert a beträgt dieser Inhalt 216 FE?

Answer 1

f_a(x) = a · √x - x   mit a>0 

a)

positive Nullstelle:  

f_a(x) = a · √x - x  = 0  ⇔  √x · (a - √x) = 0  ⇔  x = 0  oder x = a²

f_a'(x) = a / (2·√x)  - 1  →  f_a'(a²) = -1/2

Tangente in der positiven Nullstelle:   t(x) = -1/2 · ( x - a² )  = -1/2 x  +  1/2 a² 

schneidet die y-Achse in (0|3)   für a = √6 

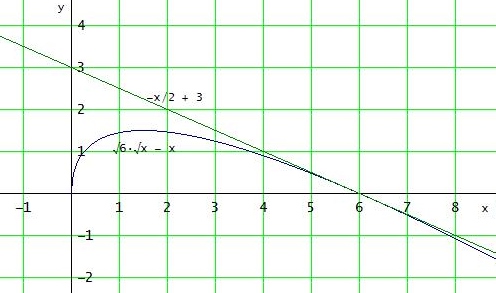
 →  f(x) = √6·√x - x   mit Tangente  t(x) = -1/2 x + 3 

b)

Fläche = \( \int\limits_{0}^{a^2} (a·\sqrt{x}-x)\text{ }dx \) = [ 2/3 a · x^3/2 - 1/2 x² ]₀^{a^2}

                  = a^4/6 = 216  →   a = 6 

Gruß Wolfgang