Zunächst muss die x-Koordinate xb des Berührpunktes B ( xb | yb ) von f ( x ) und derjenigen Tangente an f ( x ), die durch den Ursprung verläuft, bestimmt werden. Der Punkt B soll dabei im ersten Quadranten liegen. Die x-Koordinate xb von B ist dann die Obergrenze für das zu berechnende Integral.
Da die Tangente eine Ursprungsgerade ist, hat sie die Form:
t ( x ) = m x + 0
Im Berührpunkt B ( xb | yb ) müssen nun die Funktionswerte von f und t sowie die Werte derer Steigungen (Ableitungen) jeweils gleich sein. Es muss also folgendes Gleichungssystem erfüllt sein:
f ( xb ) = t ( xb ) <=> xb2 + 2 = m * xb
f ' ( xb ) = t ' ( x ) <=> 2 xb = m
Die zweite Gleichung liefert einen Term für m. Diesen setzt man in die erste Gleichung ein und erhält:
xb2 + 2 = 2 xb* xb = 2 xb2
<=> xb2 = 2
<=> xb = ± √ 2
Die negative Lösung ist unbeachtlich, da der zugehörige Berührpunkt nicht im ersten Quadranten liegt (sondern im zweiten).
Die gesuchte Tangente hat somit die Gleichung
t ( x ) = m x = 2 xb x = 2 * √ ( 2) x
Nun kann der gesuchte Flächeninhalt A berechnet werden:
A = ∫0√2 f ( x ) - t ( x ) dx
= ∫0√2 x2 + 2 - 2 * √ ( 2 ) x dx
= [ ( 1 / 3 ) x 3 + 2 x - √ ( 2 ) x 2 ]0√2
= [ ( ( √ ( 2 ) 3 / 3 ) + 2 √ ( 2 ) - √ ( 2 ) * 2 ) - ( 0 ) ]
= √ ( 2 ) 3 / 3
= √ ( 8 ) / 3
≈ 0,9428
Hier ein Schaubild von f ( x ) und t ( x ) :
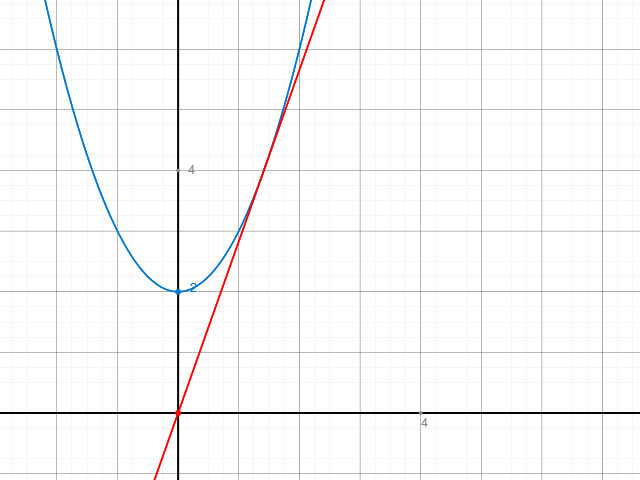
Man erkennt die zu berechnende Fläche und kann deren Flächeninhalt grob auf etwa 1 schätzen. Dies unterstützt die gefundene Lösung.