Richtig, es gibt einen "größeren" Mechanismus. Liest du dir die Lektion Satz des Pythagoras durch, stößt du auch darauf. Bzw. du siehst dir als Kunde den 3. Teil der Lektion an.
Grundsätzlich gilt:
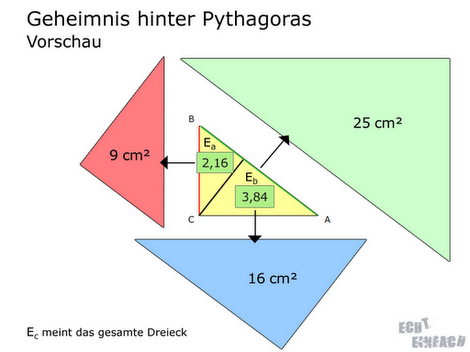
Du siehst am Beispiel, dass jede Dreiecksfläche um den gleichen Faktor mit ≈ 4,167 vergrößert wird:
2,16 cm² * 4,167 = 9 cm²
3,84 cm² * 4,167 = 16 cm²
6,00 cm² * 4,167 = 25 cm²
und du weißt sicher, dass 9 cm² + 16 cm² = 25 cm² sind bzw. 3² + 4² = 5².
Wichtig: Flächenangaben sind nicht an eine Form gebunden. Du kannst die drei vergrößerten Dreiecke also auch als Viereck, Quadrat, Fünfeck, Kreis etc. darstellen.
Um die Erklärung abzukürzen, hier der Text aus der Lektion:
Die Quadratsflächen sind nichts weiter als die drei vergrößerten Dreiecksflächen in ihrer Form verändert. Die zwei Teildreiecke Ea + Eb ergeben das gesamte Dreieck Ec, daher müssen auch die um den gleichen Faktor vergrößerten Dreiecke (dann Quadrate a² + b²) das Gesamtdreieck (dann Quadrat c²) ergeben!
Zum Weiterlesen: https://www.matheretter.de/wiki/pythagoras#prinz