Welche Querschnittsfläche hat das Flaschenprofil?

Question

Aufgabe - Design einer Flasche

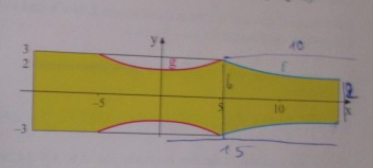
Der Querschnitt einer Flasche wird zunächst durch einen 15 cm langen Zylinder mit einem Durchmesser von 6 cm und einem 10 cm langen Flaschenhals mit der Randkurve f(x) = \( \frac{c}{x} \) modelliert.

a) Bestimmen Sie c.

b) Berechnen Sie den Durchmesser der Öffnung der Flasche.

c) Berechnen Sie das Volumen der Flasche.

Das Design der Flasche wird nun durch eine 10 cm lange und 1 cm tiefe Einbuchtung verbessert. Diese kann durch eine quadratische Funktion g(x) = ax² + bx + c modelliert werden.

d) Bestimmen Sie die Parameter a, b und c.

e) Wie groß ist das Volumen der neuen Flasche?

f) Welche Querschnittsfläche hat das Flaschenprofil? Verwenden Sie $$\int\frac{1}{x}dx=ln|x| + C$$

Ich habe die Funktionen g(x) = (1/25)x^2 + 2   und f(x)= 15/x

Wie mache ich das jetzt bei Aufgabe f?

Answer 1

Ich habe auch mal die Aufgabe gemacht. Solltest du andere Ergebnisse haben bitte um Rückmeldung

a) Bestimmen Sie c. [c = 15]

b) Berechnen Sie den Durchmesser der Öffnung der Flasche. [2 cm]

c) Berechnen Sie das Volumen der Flasche. [518.4 cm³]

d) Bestimmen Sie die Parameter a, b und c. [a = 1/25 ; b = 0 ; c = 2]

e) Wie groß wird das Volumen de neuen Flasche. [409.5 cm³]

f) Welche Querschnittsfläche hat das Flaschenprofil? [109.6 cm²]

Comments

Bei f) rechne ich

2·(∫(3, x, -10, -5) + ∫(2 + 1/25·x^2, x, -5, 5) + ∫(15/x, x, 5, 15)) = 109.6250353

---

Könntest du die Gleichung vielleicht noch mal aufschreiben... ich komme mit diesen vielen Klammern nicht klar...

---

Das ist lediglich eine völlig unbekannte Schreibweise um Integrale darzustellen ...

---

Im Integral steht zunächst die Funktion über die integriert wird, danach folgt die Integrationsvariable gefolgt von der unteren und der oberen Grenze.

In dieser Form arbeitet meine Mathematiksoftware damit. Zumindest muss ich das so eingeben. Auf dem Bildschirm wird es dann als Integral dargestellt.

---

Hier im Forum kan man LaTeX nutzen - dann sieht das so aus:

$$\int_a^b \, f(x) \, dx$$

ist aber langweilig, weil das ja keine unnötigen Rückfragen auslösen würde

---

und die ganzen Kommas?

---

∫(3, x, -10, -5) = ∫ (-10 bis -5) 3 dx

Also das Integral von -10 bis -5 über die Funktion f(x) = 3

---

achso.. okay.. danke schön

---

ich komme aber irgendwie nicht auf das ergebnis bei f)

wenn ich die zusammenrechne komme ich auf 155,64 .. was habe ich falsch gemacht?

---

Achtung. Der Faktor 2 gilt für alle 3 Integrale. Bekommst du dann das richtige heraus ?

---

nein irgendwie nicht

---

Dein 2. Integral ist auch falsch. Wie lautet die Funktion über die du da integrierst?

---

ja das habe ich auch mitgekriegt, aber wenn ich die richtige nehme, komme ich auch nicht auf die 109 FE

---

okay.. hat sich erledigt, hatte ein vorzeichen falsch gehabt

---

Könnten Sie mir die Ansätze für die   Unteraufgabrn b-e  erklären bzw. aufschreiben.Wäre echt lieb ..

---

Also b) ist ja nun so Simple, dass da ein einfaches hinschauen reicht.

c) Zylinder plus ein Rotationsintegral

d) Stelle die quadratische Funktion in der Scheitelpunktform auf. Multipliziere aus und lies die Parameter ab.

e) Ein Zylinder und zwei Rotationsintegrale.

f) ein Rechteck und 2 Integrale oder 3 Integrale.

---

Ich bin jetzt bei d

---

Ich verstehe nicht ganz was du mit der scheitelpunktform meinst ...

Im Buch stehen  2 Zahlen 1 cm und 10 cm

Muss ich damit die scheitelpunktform bilden ?

---

Du musst schauen wo der Scheitelpunkt einer dieser Parabeln liegt. Und wie groß der Öffnungsfaktor ist.

Scheitelpunkt bei S(0|2) ein weiterer Punkt bei P(5|3)