Aufgabe:
7.1.0 Auf einem Gelände, dessen Begrenzung durch den Graphen \( \mathrm{G}_{\mathrm{f}} \) der Funktion \( f \) mit der Gleichung \( \mathrm{f}(\mathrm{x})=-\frac{1}{10}\left(\mathrm{x}^{2}-200 \mathrm{x}\right) \) und der Abszissenachse beschrieben werden kann, soll zu Forschungszwecken ein rechteckiges Versuchsfeld \( A B C D \) mit maximalem Flächeninhalt eingerichtet werden.
Eine Gerade \( \mathrm{x}_{1}=100-\mathrm{u} \) schneidet die Abszissenachse im Punkt \( \mathrm{A} \) und den Graphen \( \mathrm{G}_{\mathrm{f}} \) im Punkt \( \mathrm{D} \).
Eine weitere Gerade \( \mathrm{x}_{2}=100+{u} \) schneidet die Abszissenachse im Punkt \( \mathrm{B} \) und \( \mathrm{G}_{f} \) im Punkt \( C \).
Für u gilt: \( u \in \mathbf{R} \) und \( 0<{u}<100 \).
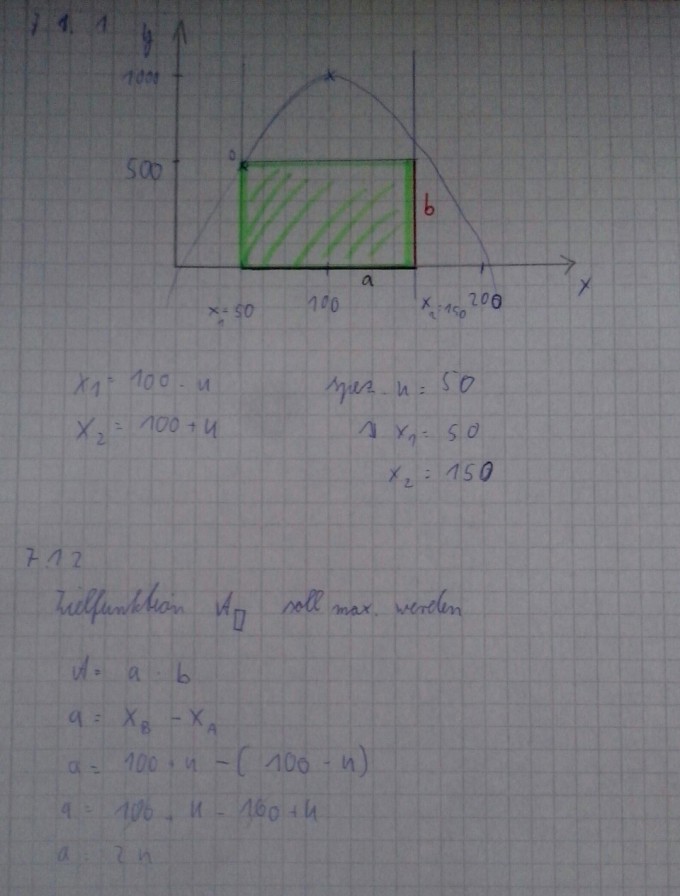
7.1.1 Skizzieren Sie diesen Sachverhalt für den Sonderfall \( {u}=50 \) in ein geeignetes Koordinatensystem.
7.1.2 Weisen Sie rechnerisch nach, dass die Funktion A mit der Gleichung
\( \mathrm{A}(\mathrm{u})=-\frac{1}{5} \mathrm{u}^{3}+2000 \mathrm{u} \)
eine Zielfunktion für die Berechnung des Flächeninhalts des Versuchsfelds ist.
7.1.3 Bestimmen Sie rechnerisch den Wert für \( u \) so, dass der Flächeninhalt des Versuchsfelds maximal wird. (Auf die Überprüfung der Randwerte wird verzichtet.)
7.1.4 Als Maßstab gilt: \( 1 \mathrm{LE}=1 \mathrm{~m} \). Geben Sie die Seitenlängen des Versuchsfelds in Meter und dessen maximalen Flächeninhalt in Hektar an.
7.2.0 Vom Versuchsfeld geerntete Grünfuttersorten sollen in geschlossenen zylinderförmigen Behältern zwischengelagert werden. Diese müssen bei einem Fassungsvermögen von 4000 Litern eine minimale Oberfläche aufweisen.
7.2.1 Zeigen Sie rechnerisch, dass die Funktion \( \mathrm{A}_{\mathrm{o}} \) mit der Gleichung
\( \mathrm{A}_{\mathrm{O}}(\mathrm{r})=2 \pi \mathrm{r}^{2}+\frac{8}{\mathrm{r}} \)
eine Zielfunktion fïr die Berechnung des Oberflächeninhalts in Quadratmeter eines der in 7.2.0 beschriebenen Behälter ist.
7.2.2 Geben Sie die erste und zweite Ableitung der Zielfunktion und den minimalen Oberflächeninhalt eines Behälters an.
Ansatz/Problem:
Die Aufgaben 7.1.1 und 7.1.2 hab ich schon gelöst (Ansatz lade ich gleich mit hoch). Nun hab ich irgendwie keinen Plan mehr von den anderen Aufgaben. Denkanstöße, Lösungsansätze oder Komplettlösungen egal was ihr mir liefern könnt, ich bin mit allem zufrieden.