Boden eines 2 km langen Kanals hat die Form einer Parabel. Querschnittsfläche?

Question

Aufgabe:

Der Boden eines 2 km langen Kanals hat die Form einer Parabel. 1LE = 1km

a) Berechnen Sie den Inhalt der Querschnittsfläche des Kanals

b) Bestimmen Sie das Wasservolumen des ganz gefüllten Kanals

c) Berechnen Sie, wie viel Prozent der maximalen Wassermenge sich im Kanal befindet, wenn er nur bis zur halbem Höhe gefüllt ist.

Integralrechnung/eventuell Vektorrechnung? Zum Beispiel verstehe ich nicht, wieso man bei a) den Punkt (4|2) verwenden muss oder vor dem Integral 16- schreiben muss.

Comments

Vom Duplikat:

Titel: Funktionsgleichung einer Parabel aufstellen. Querschnittsfläche eines Kanals

Stichworte: funktionsgleichung,kanal,parabel,wasserstand,integralrechnung,prozentrechnung

Hallo. Die Aufgabe ist:

Der Boden eines 2km langen Kanals hat die Form einer Parabel. Dabei entspricht einer Längeneinheit 1m in Wirklichkeit.

Foto: ps. Ich hab da schon rum gekritzelt.

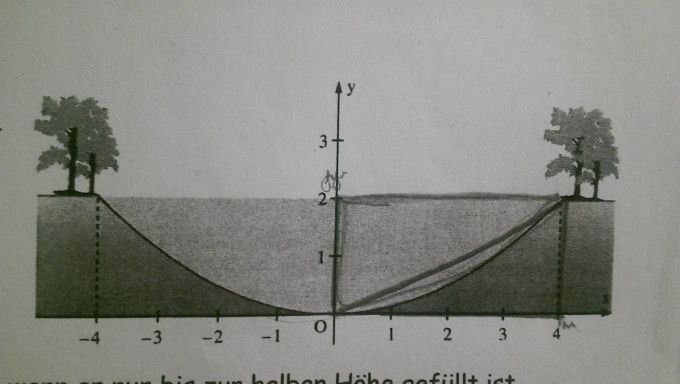
a) berechnen sie den Inhalt der Querschnittsfläche des Kanals

b) wie viel Wasser befindet sich im Kanal, wenn er ganz gefüllt ist?

C) wieviel Prozent der maximalen Wassermenge befindet sich im Kanal , wenn er nur bis zur halben Höhe gefüllt ist ?

meine eigenen Fragen dazu Sind:

1. Ist die 2 auf der y-Achse eine km Angabe der lange des Kanals oder sind das nur 2 Meter Wasserstand ?

2. Wie beweise ich dass die Funktion eine Steigung von 1/8 hat ? Ich habe es rausgefunden aber mir fällt keine Formel ein für m (ausser Mx+b) doch diese Formel gilt doch nur für geradengleichungen oder gibt es auch eine für quadratische ?

danke im voraus.

---

Vom Duplikat:

Titel: Berechnen Sie den Inhalt der Querschnittsfläche des Kanals.

Stichworte: integralrechnung,kanal,parabel

Aufgabe: Kanalquerschnitt
Der Boden eines 2 km langen Kanals hat die Form einer Parabel mit der Gleichung f(x) = 0,125x2. Dabei entspricht eine Längeneinheit 1 m in der Wirklichkeit.
a) Berechnen Sie den Inhalt der Querschnittsfläche des Kanals.
b) Wie viel Wasser befindet sich im Kanal, wenn er ganz gefüllt ist?
Abbildung 2:
c) Wie viel Prozent der maximalen Wassermenge befindet sich im Kanal, wenn er nur bis zur halben Höhe gefüllt ist?

Problem/Ansatz:

Ich verstehe diese Aufgabe nicht, kann mir bitte jemand diese Aufgabe erklären, mit einem Lösungsweg!

Vielen Dank!

P.S. das Thema ist Integralrechnung

---

Hallo

hier gibt es wohl schon eine Zeichnung, sonst braucht man noch die Breite des Kanals, angenommen er ist 10m breit, dann muss man von der Fläche  des Rechtecks f(5)*10 die Flache unter der Parabel abziehen also das Integral von -5 bis +5.

bitte poste immer die ganze Orginalaufgabe.

Gruß lul

---

Dies ist die Skizze dazu

---

Vom Duplikat:

Titel: Bestimmen Sie rechnerisch die Querschnittsfläche des Kanals.

Stichworte: integralrechnung,funktionsgleichung,parabel,kanal

Aufgabe:

Der Boden eines 2km langen Kanals hat die Form einer Parabel. (Eigentlich Abbildung, allerdings neu hier und will mich nicht strafbar machen, indem ich sie hochlade).

Dabei entspricht eine Längeneinheit 1m in der Wirklichkeit.

a) Bestimmen Sie rechnerisch die Querschnittsfläche des Kanals.

b) Wie viel Wasser befindet sich im Kanal, wenn er vollständig gefüllt ist?

Problem/Ansatz:

zu a) die Aufgabe habe ich verstanden und das Ergebnis ist 10,33 m^2

zu b) in den Lösungen steht man berechne hier V = G • h  also  V = 10,33 • 2000 (Länge des Kanals)

Meine Frage zu b : Wie komme ich auf die Formel V= G • h ?

---

Hallo.

Ich bearbeite gerade ebenfalls die Aufgabe und ich habe eine Frage zu Aufgabenteil a.

Eigentlich kann es nur so sein, aber stimmt es dann, dass die erhaltene Querschnittsfläche die Fläche oberhalb der Parabel ist?

Vielen Grüße

---

Hmm, das ist etwas vage um es sicher zu beantworten. Aber:

Wenn Du einfach das Integral in den Grenzen von -4 bis 4 berechnest, dann betrachtest Du nur den gelben Teil zwischen x-Achse und der Funktion. Wir sind hier aber am grünen Teil interessiert. Wir stellen uns also vor, dass wir ein Rechteck haben, dass die Seitenlänge 8 (an der x-Achse) und die Seitenlänge 2 (y-Achse) hat. Wenn wir von diesem Rechteckflächeninhalt den gelben Teil abziehen, verbleibt der grüne Teil.

Das siehst Du dann auch bei den anderen Antworten unten: Flächeninhalt = 16 - Integral.

Alles klar?

---

Jetzt bin ich gerade um ehrlich zu sein etwas verwirrt.

Was genau meinst du mit „grüner Teil“?

---

Oder blau. Sieht man nicht so eindeutig auf meinem Bildschirm. Ich spreche vom "Kanal". Siehe obiges Schaubild.

---

Oki dann ist alles klar.

Danke für Deine Hilfe ! :)

---

was ist der kanal ? das reckteck, das blaue, das gelbe ??

---

Der Querschnitt des Kanals wird durch die blaue Fläche dargestellt.

Answer 1

1. das sind 2 m Wasserstand (Querschnittszeichnung)

2. die Parabel geht durch den Punkt (4/2) und die Parabel geht durch den Ursprung

allgemein gilt für die Parabelgleichung: y=a*x -> a=y/x = 2/4 -> a=0,5

daher lautet die Gleichung y=0,5*x²

Die Steigung ist die erste Ableitung f'(x)=a*n*x^_(n-1)

-> y'= 2*0,5*x

y'= x

wozu brauchst du die Steigung?

Frank

Comments

Wenn ich diese Funktion in den Taschenrechner eingebe und eine wertetabelle erstelle, entsprechen die y Werte der Tabelle nicht der parabel. Deswegen muss die steigung 1/8 sein um der parabel zu entsprechen ...

---

Das stimmt so nicht, da nur bei einer Geraden die Steigung immer konstant ist

---

Zitat von Frank B.: "allgemein gilt für die Parabelgleichung: y=a*x <=> falsch!!

korrekt wäre y = a*x² =>  a=y/x² = 2/16 -> a=1/8 
daher lautet die Gleichung y=1/8*x²
Also Fläche A =  -4 bis 4 über 1/8*x² dx ; A = ... m²
V = A*l => ... m² * 2000 m = ... m³

---

sorry, stimmt hatte die Potenz vergessen.

Aber für die Berechnung der Querschnittsfläche muss von dem eingeschlossenen Rechteck die Fläche der unter der Parabel abgezogen werden und diese Fläche mit 2000m multipliziert werd.

---

Ok also die Funktion hab ich jetzt schon mal erläutert, d.h. die 1/8 waren richtig . Danke . Zu Aufgabe a ) hab ich alles verstanden. Wir haben am Ende dann ein Volumen wenn ich das mit den 2 km multipliziere hab ich recht ?

zu Aufgabe b) habe ich auch keine Fragen, aber wie löse ich Aufgabe c) ?

---

somit F(Rechteck)=2m*8m=16m²

abzüglich _-4⁴∫1/8*x² dx = [1/24*x³]_-4⁴=....64/24+64/24=5 1/3

-> V=(16-5 1/3)*2000 m³= 21333,33.... m³

---

Fläche des Querschnitts aus b) hast du ja.

jetzt mußt du die Querschnittsfläche des halb gefüllten Kanals ausrechnen (Füllstand 1 m)

y=1/8*x²

y=1 -> x²=8, x= 2√2

-> F(halbvoll)=-_2√2^2√2∫1/8*x² dx

F(halbvoll)/Fvoll*100 (aus Aufgabe b) = Prozent der maximalen Wassermenge befindet sich im Kanal , wenn er nur bis zur halben Höhe gefüllt ist

---

Hallo Frank b. Wofür muss ich denn bei Aufgabe b) den Flächeinhalt des rechtecks, dem integral abziehen ? Wenn ich das integral setze und die stammfunktion bilde ziehe ich doch automatisch die Fläche unterhalb und oberhalb ab ?

---

Entweder, du machst das so, wie georgborn vorgeschlagen hat (er hat die elegantere Lösung präsentiert), oder du machst es wie ich vorgeschlagen habe als "Zweiteiler" Da das Integral die Fläche unter der Funktion berechnet musst du diese Division durch führen.

LG Frank

Answer 2

a) berechnen sie den Inhalt der Querschnittsfläche des Kanals

Es handelt sich um eine Parabel mit dem
allgemeinen Funktionsterm

f ( x ) = a * x^2
f ( 4 ) = a * 4^2 = 2
a = 1 / 8
f ( x ) = 1/8 * x^2

Die Fläche wird über die Integralrechnung ermittelt

Stammfunktion
S ( x ) = ∫  a * x^2 dx
S ( x ) = 1 / 8 * x^3 / 3
S ( x ) = 1 / 24 * x^3

F = [ S ( x ) ] _-4 ⁴
F = [ 1 / 24 * x^3 ] _-4 ⁴
F = 1 / 24 * 4^3 - 1 / 24 * (-4)^3
F = 16 / 3 m^2

b) wie viel Wasser befindet sich im Kanal,
wenn er ganz gefüllt ist?

V = Grundfläche * l
V = 16 / 3 m^2 * 2000 m
V = 10667 m^3

C) wieviel Prozent der maximalen Wassermenge
befindet  sich im Kanal , wenn er nur bis zur
halben Höhe gefüllt ist ?

f ( x ) = 1 / 8 * x^2 = ( 2 m / 2 )
1 / 8 * x^2 = 1
x^2 = 8
x = √ 8

F = [ 1 / 24 * x^3 ] _{-√ 8} ^{√ 8}
F = 1.8856 m^2

1.8856 / ( 16 / 3 )
0.3535
35.35 %

mfg Georg

Comments

Danke Georg, genau so in ich auch vorgegangen

 Jetzt bin ich mir der Richtigkeit sicher

---

Fehlerkorrektur

F = 16 / 3 m²

Dies ist die Fläche unterhalb der Funktion.

Das die Funktion umgebende Rechteck ist
R = 8 * 2 = 16 m^2

Kanalfläche
16 - 16 / 3  = 32 / 3 m^2

b) wie viel Wasser befindet sich im Kanal,
wenn er ganz gefüllt ist?

V = Grundfläche * l
V = 32 / 3 m² * 2000 m
V = 21333 m³

C) wieviel Prozent der maximalen Wassermenge
befindet  sich im Kanal , wenn er nur bis zur
halben Höhe gefüllt ist ?

f ( x ) = 1 / 8 * x² = ( 2 m / 2 )
1 / 8 * x² = 1
x² = 8
x = √ 8

F = [ 1 / 24 * x³ ] _{-√ 8} ^{√ 8}
F = 1.8856 m²

Dies ist  Fläche unterhalb der Kurve

Das diese Fläche ummgebende Rechteck ist
R = 2 *  √ 8 * 1 = 5.6568 m^2

Wasserfläche bei h = 1
5.6568 - 1.8856 = 3.7712 m^2

 3.7712  / ( 32 / 3 )
0.3535
35.35 %

---

Ich dachte wenn ich integriere und F(b)-F(a) rechne kommt schon der flächeninhalt der parabell raus und nicht die Fläche unter der parabell ?

---

Dies wäre die Skizze

Wllist du die Kanalwasserfläche direkt berechnen kannst du
auch die Höhe der Wasseroberläche minus die Funktion
als Differenzfunktion  aufstellen.

d ( x ) = 2 - f ( x )
∫ 2 - 1/8 * x^2 dx zwischen -4 und 4

mfg

---

Aber warum ergibt das integral -4 bis 4 die Fläche unter dem Kanal ? Und nicht die Fläche der parabel das verstehe ich nicht.

---

Weil integrale immer die Fläche unter der Kurve angeben.

Answer 3

f(x) = a*x^2 und mit Einsetzen von P(4/2) gibt es a= 1/8

Also Fläche A = 16 - Integral von -4 bis 4 über 1/8x dx gibt dann 10,667
b) V = A*Länge = 10,667 * 2000 = 21333
c) halbe Höhe:
1/8 x^2 = 1 gibt x = + oder - wurzel(8)

Fläche dann 2*wurzel(8)*1    -   integral von -wurzel(8) bis wurzel(8) über 1/8x dx gibt dann 3,771
Volumen also 3,771*2000 = 7542

Comments

Dankeschön! Leider verstehe ich nicht wie Sie auf die Funktion a*x^2 gekommen sind und den Punkt P?

Außerdem tu ich mich mit der Rechnung in a und c etwas schwer beim nachvollziehen? Was genau stellt die Rechnung dar?:( Also ich bin etwas ungeübt mit Integralen...:)

---

mathef meinte hier

"Also Fläche A = 16 - ∫_(-4) ^4  1/8 x^2 dx gibt dann 10,667"

Also ein x^2 im Integranden.

---

Wie schon von Lu korrigiert.  sollte natürlich  1/8 x^2  sein.

Parabeln mit dem Scheitel im Nullpunkt haben immer Gleichungen

der Form  y = a*x^2  nur der Faktor vor dem x^2 ist unterschiedlich und gibt

sozusagen die "Breite" oder "Schmalheit" der Parabel an.

Auf der Zeichnung siehst du, dass deine Parabel durch den Punkt (4/2) geht.

Wenn du nun bei   y = a*x^2 für x=4 und y=2 einsetzt, kannst du das a ausrechnen

und hast die Parabelgleichung  y = 1/8 x^2

Answer 4

Zu Parabelngleichungen solltest du unbedingt erst die Theorie nochmals anschauen.

vgl. hier: https://www.matheretter.de/wiki/quadratische-funktionen

oder gleich im Einführungsvideo:

https://www.youtube.com/watch?feature=player_embedded&v=BeXmLxAicPg

Sobald du deine Gleichung hast, kannst du dich dann um die Integration kümmern.

Answer 5

Das Bild passt nicht zum Text. Im Text ist 1 LE= 1km. Wenn das  auch im Bild gilt, wäre der Kanal 8 km breit und die Bäume 2km hoch.

a) Zunächst muss die Gleichung der Parabel berechnet werden. Ansatz f(x)=ax ². Der Punkt (4|2) liegt auf der Parabel. Dann ist a=1/4 und die Parabelgleichung lautet f(x)=x²/4.

Das Bild zeigt offenbar die Querschnittsfläche des Kanals. die man so ausrechnen kann 2·(8-∫(x²/4)dx in den Grenzen von 0 bis 4). Also F=16/3.

b) Um das Volumen des Kanals zu bestimmen,gehe ich davon aus, dass die Querschnittsfläche in m² berechnet wurde. Dann ist das Volumen 16000/3 m³.

Answer 6

Hallo

von der Parabel kennst du den Scheitel bei 0 und den Wert 2 bei x=4 also hast du y=a*x^2 und willst a also 2=a*4^2 a=1/8

für die Fläche musst du dann von dem Rechteck Breite 8 Höhe 2 also Fläche 16km^2 das Integral von -2 bis 2 der Parabel y=1/8*x^2 abziehen.

war das die Frage?

Gruß lul

Answer 7

Kanalquerschnitt

Der Boden eines 2 km langen Kanals hat die Form einer Parabel mit der Gleichung f(x) = 0,125x2. Dabei entspricht eine Längeneinheit 1 m in der Wirklichkeit.

a) Berechnen Sie den Inhalt der Querschnittsfläche des Kanals.

A = ∫ (-4 bis 4) (2 - 0.125·x^2) dx = 32/3 = 10 2/3 m²

b) Wie viel Wasser befindet sich im Kanal, wenn er ganz gefüllt ist?

A*h = 32/3·2000 = 21333 m³

c) Wie viel Prozent der maximalen Wassermenge befindet sich im Kanal, wenn er nur bis zur halben Höhe gefüllt ist?

A2 = ∫ (- 2·√2 bis 2·√2) (1 - 0.125·x^2) dx = 8/3·√2 = 3.771

8/3·√2 / (32/3) = √2/4 = 0.3536 = 35.36%

Answer 8

Wenn du dir den Kanal senkrecht hingestellst denkst,

dann ist es so ähnlich wie eine Prisma mit der

Grundfläche = Querschnittsfläche und mit der Höhe=Kanallänge