Zeichne das Muster für n = 4. Gib die Anzahl der Sternchen in diesem Muster an.

Question

Aufgabe:

Jeder positiven ganzen Zahl $n$ wird ein Muster aus Sternchen wie folgt zugeordnet: In einem quadratischen Gitternetz befinden sich beim $n$-ten Muster $2 n-1$ Sternchen auf horizontal benachbarten Gitterpunkten. Die weiteren Sternchen befinden sich derart auf Gitterpunkten, dass sich ein quadratisches Muster ergibt, bei dem diese $2 n-1$ Sternchen die horizontale Diagonale bilden. Für $n=1,2,3$ sind die Muster in der Abbildung dargestellt.

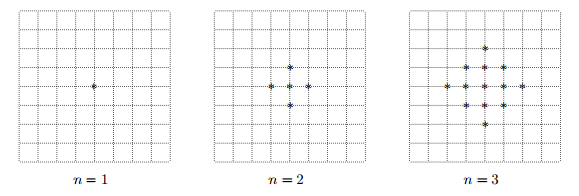
a) Zeichne das Muster für $n=4$. Gib die Anzahl der Sternchen in diesem Muster an.

b) Ermittle die Anzahl der Sternchen im Muster für $n=10$.

c) Ermittle eine Formel, mit deren Hilfe man die Anzahl der Sternchen für jedes beliebige $n$ ausrechnen kann. Berechne mit dieser Formel die Anzahl der Sternchen für $n=30$.

d) Untersuche, ob es eine Zahl $n$ derart gibt, dass das $n$-te Muster 318 Sternchen mehr enthält als das vorangegangene Muster.

Ansatz/Problem:

Da ich dazu keine Lösungen finde, wollte ich wissen ob ihr meine Lösungen kontrollieren könntet.

a) Bei a hatte ich 25 Sterne gezählt.

b) Ich bin mit der Formel, die ich in c) herausgefunden hatte, auf 181 gekommen.

c) Ich habe hier 2 Formeln gefunden. Bei der ersten muss man die vorherige Anzahl Sterne wissen, die zweite ist Allgemeingültig.

Anzahl Sterne = S    InI = Anzahl Sterne vom n-ten Muster

(1) S=In-1I+4(n-1)

(2) S=2(n-1)*n+1

hier noch vereinfacht:

(2) S=2n²-2n+1

Mit dieser Formel, bin ich darauf gekommen, das bei n=30, die Anzahl Sterne 1741 ist.

d) Hier bin ich auf diese Gleichung gekommen: 2(n-1)*n+1-318=2(n-2)*(n-1)+1, da n dann 80,5 gibt es keine Zahl n derart

Comments

s1 = 1,

s2 = 5 = 1 + (8-4)

s3 = 5 + (12-4) = 13

s4 = 13 + (16 - 4) = 25

Meine Rekursionsformel wäre:

s_(n+1) = s_(n) + (4*(n+1)-4) = s_(n) + 4n

Deine explizite Formel:

Sn=2n²-2n+1

sn+1 = 2(n+1)²-2(n+1)+1

sn+1 - sn = 2(n+1)²-2(n+1)+1 - (2n²-2n+1)

= 2(n² + 2n + 1) - 2n -2 + 1 - 2n² + 2n - 1

= 2n² + 4n + 2 - 2n - 1 - 2n² + 2n -1

= 4n 

Deine Formel stimmt auch beim Nachrechnen:

Sn=2n²-2n+1

s1=1

s2 = 8 - 4 + 1 = 5

s3 = 18 - 6 + 1 = 13

s4 = 32 - 8 + 1 = 25

d) 318 = 4k geht nicht, da 318 nicht durch 4 teilbar ist, kann es den Unterschied von exakt 318 nicht geben. Bestätigt deine Folgerung.

Ich nehme an, dass du bei b) und c) richtig eingesetzt hast.

---

http://www.mathematik-olympiaden.de/aufgaben/53/3/A53073b.pdf

Vermutlich sind dazu auch Lösungen veröffentlicht worden, aber es ist sicherlich viel schöner, sich ohne Rückgriff auf die Lösungen damit zu beschäftigen.

---

Danke für deine schnelle und ausführliche Antwort :-)

---

Gibt es eigentlich einen schnellen Lösungsweg, mit dem man solche Formeln finden kann? Ich habe einfach Die Verhältnisse der sternen analysiert und regelmässikeitn gesucht

---

"Ich habe einfach Die Verhältnisse der sternen analysiert und regelmässikeitn gesucht"  Das ist mE der schönste Ansatz. Anhand der Form kann man schon mal davon ausgehen, dass n² in der Formel reinkommen muss.

Eine mögliche Vereinfachung:

Bei linearer Zunahme der Summanden, kannst du annehmen, dass eine quadratische Funktion die Summenfolge sn beschreibt. (Allg. Grad des Terms um 1 erhöhen)

Also sn=  a*n² + b*n + c ansetzen und ausprobieren, wie du es vermutlich gemacht hast.

Das geht so ähnlich wie beim Integrieren.

f(n) = 4n

F(n) = 2n² + D

und dann noch irgendwie den linearen Anteil (also b und c) der Lösung bestimmen.

Du kannst auch in sn = a*n² + b*n + c einfach 3 bekannte Punkte einsetzen und dann ein LGS mit 3 Unbekannten lösen.

---

Man darf wissen: Die Summe der ungeraden Zahlen

1 + 3 + 5 + (2n - 1) = n²

Das entspricht hier genau dem oberen Dreieck. Nehme ich das mal 2 und subtrahiere ich die (2n - 1) Sterne die ich dann doppelt gezählt habe erhalte ich

2n² - (2n - 1) = 2n² - 2n + 1

Aber es ist hier natürlich erlaubt jeden beliebigen Weg zu wählen. Es gibt über 100 verschiedene Methoden den Satz des Pythagoras zu begründen. Es langt meist wenn man einen geeigneten Weg wählt.

Answer 1

Zitat:

(2) S=2(n-1)*n+1

hier noch vereinfacht:

(2) S=2n²-2n+1

Mit dieser Formel, bin ich darauf gekommen, das bei n=30, die Anzahl Sterne 1741 ist.

Zitat Ende.

Ich forme die zuletzt genannte Formel mal etwas um:
$$S(n) = 2n^2-2n+1 = n^2+n^2-2n+1 = n^2 + \left(n-1\right)^2$$Jetzt zeigt sich, dass die $S(n)$ jeweils die Summe zweier aufeinanderfolgender Quadratzahlen sind. Nachrechnen mit dieser Formel ergibt die Folge: $\begin{pmatrix}1,&5,&13,&25,&41,&\dots\end{pmatrix}$ und speziell $S(10) = 10^2+9^2 =181$ bzw. $S(30) = 30^2+29^2 = 900+841 = 1741$.

Aufgabenteil d fragt nach den ganzzahligen Lösungen der Gleichung $S(n)-S(n-1)=318$ und mit $S(n) = n^2 + \left(n-1\right)^2$ lässt sich leicht zeigen, dass die linke Seite immer durch 4 teilbar ist, die rechte jedoch nicht.

Diese Zahlen heißen "zentrierte Quadratzahlen" und kommen neben anderen "figurierten" Zahlen gelegentlich auch im Schulunterricht vor. Mehr dazu:

http://mathworld.wolfram.com/CenteredSquareNumber.html

https://de.wikipedia.org/wiki/Zentrierte_Quadratzahl

http://oeis.org/A001844

http://www.mathematische-basteleien.de/figuriertezahlen.htm#Zentrier…