wie lautet diese Funktion? Hilfe

Question

Kann mir vielleicht jemand sagen wie die Funktion heisst?? ich komm einfach nicht drauf

Answer 1

Das ist die Dichtefunktion eines Stoffes der etwas schwerer als Wasser ist.

Aufgetragen ist die Dichte eines Stoffes in Abhängigkeit zu seiner Temperatur.

Comments

ja das das eine Dichte Funktion ist weiss ich aber ich muss irgendwie die Funktion rausbekommen damit ich in excel weiter rechnen kann

---

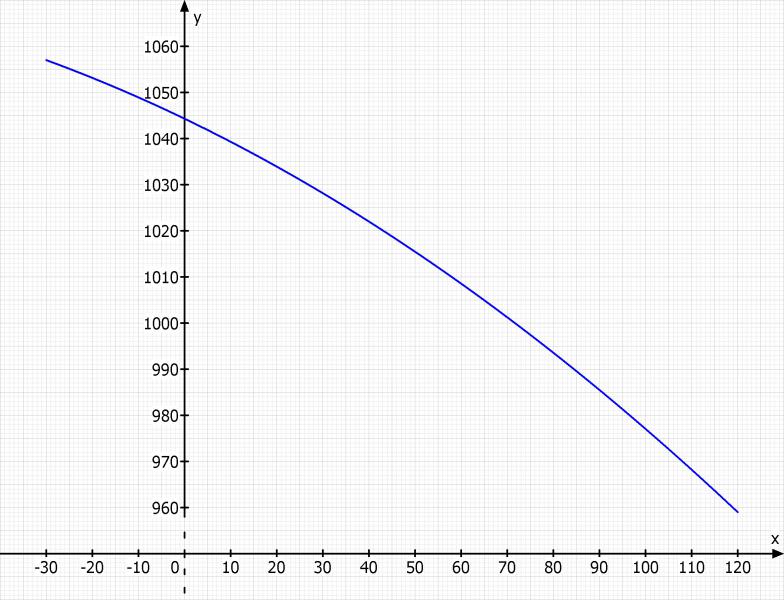
Je nachdem wie genau das sein muss kann man es z.B. auch durch eine Parabel annähern. Dazu würde man sich drei Punkte suchen

P(-30 | 1057)
Q(40 | 1022)
R(120 | 959)

f(x) = ax^2 + bx + c

f(-30) = 1057 ---> 900·a - 30·b + c = 1057
f(40) = 1022 ---> 1600·a + 40·b + c = 1022
f(120) = 959 ---> 14400·a + 120·b + c = 959

Das ist ein lineares Gleichungssystem was man durch Additionsverfahren lösen kann.

Die Lösung ist hier: a = -23/12000 ∧ b = -577/1200 ∧ c = 10443/10

Man könnte also im Bereich von -30 bis 120 die Dichtefunktion annähern durch

 

f(x) = -23/12000*x^2 - 577/1200*x + 10443/10

Hier mal eine Skizze dieser Funktion: