Extremwert Rechteck in Quadrat (a*a) eingeschoben

Question

Es will einfach nicht funktionieren....

Hallo, ich habe wieder eine Frage zu einer Extremwertaufgabe:

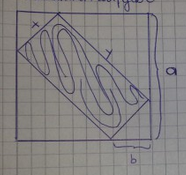
Das Rechteck mit A ⇒ max. soll in ein Quadrat mit der Seitenlänge a eingeschrieben werden.

$\begin{aligned} A &=a^{2}-b^{2}-(a-b)^{2}=2 a b-2 b^{2} \end{aligned}$

Weiter weiß ich nicht. Mir fehlt eine Nebenbedingung. Könnt ihr mir bitte helfen? Danke.

Answer 1

A (b) = 2ab - 2b²

Wiederum ist a konstant und b variabel.

A'(b) = 2a - 4b = 0

==> b = a/2

Weiter mit Pythagoras kommst du auf:

-> x = y = (√2 * a)/2