Lagrange-Multiplikator ausrechnen

Question

Die Nutzenfunktion eines Individuums lautet U(x1,x2)=60(ln)x1+60(ln)x2. Gegeben sind die Preise der beiden Güter p1=1 und p2=1. Minimieren Sie die Kosten des Individuums, wenn ein Nutzenniveau von 530 erreicht werden soll.

Wie hoch ist der Lagrange-Multiplikator λ im Kostenminimum?

Answer 1

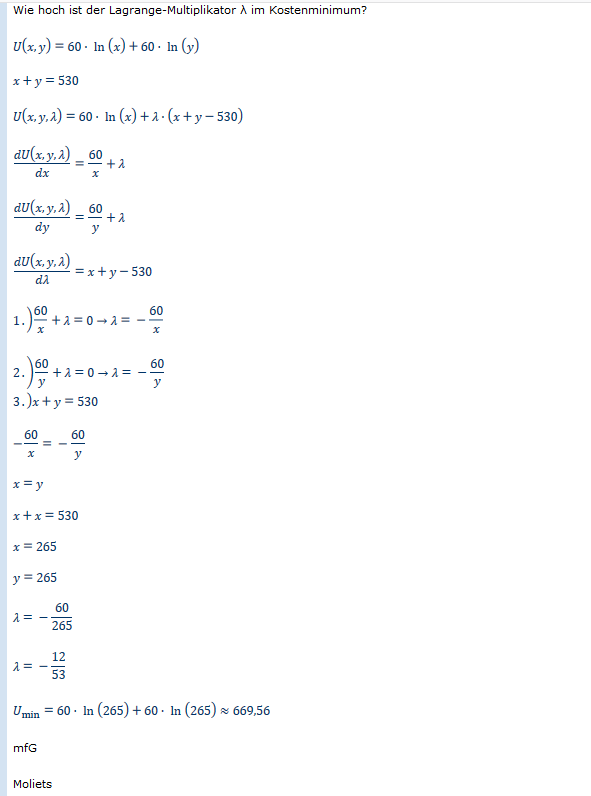
Text erkannt:

Wie hoch ist der Lagrange-Multiplikator $\lambda$ im Kostenminimum?
$U(x, y)=60 \cdot \ln (x)+60 \cdot \ln (y)$
$x+y=530$
$U(x, y, \lambda)=60 \cdot \ln (x)+\lambda \cdot(x+y-530)$
$\frac{d U(x, y, \lambda)}{d x}=\frac{60}{x}+\lambda$
$\frac{d U(x, y, \lambda)}{d y}=\frac{60}{y}+\lambda$
$\frac{d U(x, y, \lambda)}{d \lambda}=x+y-530$
1. $) \frac{60}{x}+\lambda=0 \rightarrow \lambda=-\frac{60}{x}$
2. $) \frac{60}{y}+\lambda=0 \rightarrow \lambda=-\frac{60}{y}$
3. $) x+y=530$
$-\frac{60}{x}=-\frac{60}{y}$
$x=y$
$x+x=530$
$x=265$
$y=265$
$\lambda=-\frac{60}{265}$
$\lambda=-\frac{12}{53}$
$U_{\min }=60 \cdot \ln (265)+60 \cdot \ln (265) \approx 669.56$
mfG
Moliets