Trapez dreht sich um Parallelseite. Berechnen Sie die Längen der Seiten und der Diagonalen.

Question

Ansatz/Problem:

Ein gleichschenkeliges Trapez mit dem Umfang 32 cm dreht sich einmal um die eine, dann um die andere Parallelseite. Die Volumina der beiden Drehkörper verhalten sich wie 5:6, die Oberflächen wie 29:35.

(a) Fertigen Sie eine Skizze an.

(b) Berechnen Sie die Längen der Seiten und der Diagonalen.

(c) Berechnen Sie die Winkel an den Eckpunkten und zwischen den Diagonalen.

(d) Berechnen Sie die Fläche des Trapezes.

Answer 1

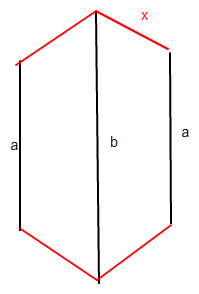
Erst mal Längsschnitt durch den Drehkörper beim drehen um die

lange Seite :   (geht gleich weiter)

32 = a+b+2x gibt x=16 - 0,5a - 0,5b    

und die Trapezhöhe h ist ja der Radius für die Drehkörperteile ist

h^2 = x^2 -  ( (b-a)/2 )^2   = ab - 16a - 16b + 256

Volumen der oberen und unteren Kegel

V = 1/3*pi  * r^2 * h    und der Zylinder in der Mitte V = pi* r^2 * a

also zusammen 2/3 pi** r^2 * h   + pi* r^2 * a  = pi* r^2 * ( 2/3 * (b-a)/2   +  a )

= 2/3*pi * (ab - 16a - 16b + 256) * (b-a)/2 =pi* (2a+b)*(b-16)*(a-16)  / 3

Beim Drehen um die kurze Seite ist es ähnlich, nur die Kegel werden

vom Zylinder subtrahiert,  gibt

V =  - 2/3*pi * r^2 * h   +   r^2 * a  = r^2*pi* ( a  - 2/3 *  (b-a)/2    ) = pi* (4a-b)*(b-16)*(a-16)  / 3

Das Verhältnis ist also ( 2a+b)  /  (4a-b )

Mantel des Drehkörpers ist in beiden Fällen mit dem oben berechneten h als Radius

M1=2*pi*r*a  = 2*pi*a *wurzel( ab - 16a - 16b + 256)   und 

M2= 2*pi*r*b = 2*pi*b*wurzel( ab - 16a - 16b + 256)

Grund und Deckflächen sind jeweils die Kegelmäntel

M3= pi*r*s  = pi*wurzel( ab - 16a - 16b + 256)*(16 - 0,5a - 0,5b    )

Ich glaube fast, dass dies wohl ein zu komplizierter Ansatz ist;

denn auch wenn man das Verhältnis ( 2a+b)  /  (4a-b ) = 6 / 5

nach b = 14/11 * a auflöst und einsetzt, kommt mir das noch arg lang vor.

Comments

Ja ok hab ich mir auch gedacht aber wie komme ich auf die?
Mich verwirrt das mit den Verhältnissen .

---

Nimm einfach ein Trapez mit Grundseite b, Oberseite a und Höhe h. Stelle dafür jetzt die Volumen und die Ratationskörperformel auf. Dann noch eine Gleichung für den Umfang. Das gibt 3 Gleichungen mit 3 Unbekannte, welches du dann sicher lösen kannst.

Answer 2

Nimm einfach ein Trapez mit Grundseite b, Oberseite a, Höhe h und Schenkel s. Stelle dafür jetzt die Volumen- und die Oberflächenformel des Rotationskörpers auf. Dann noch eine Gleichung für den Umfang. Das gibt 3 Gleichungen mit 3 Unbekannte, welches du dann sicher lösen kannst.

Ich habe folgende Lösung heraus: a = 4 ∧ b = 7 ∧ s = 10.5

Comments

So muss es gehen ja! Nur wie bekomme ich die Volumen und Rotationskörperformel?

---

Könntest du mir vl ein Foto oder screenshot deiner Lösung kommentieren?
Steh noch immer am Schlauch :/

---

Wie sieht denn der Rotationskörper aus ? Du solltest dir das mal aufzeichnen.

mathef hat dir schon so eine schöne Skizze gemacht.

Der Rotationskörper lässt sich aus 2 ganz einfachen geometrischen Körpern zusammensetzen.

---

Rotationsvolums formel habe ich jetzt :)
Aber was meinst du mit der normalen Volumsformel das habe ich noch nicht verstanden?
Umfang ist auch klar!
Die Skizze hat echt geholfen danke!

---

Du brauchst nur die Formel für das Rotationsvolumen der beiden Rotationskörper. Daraus bildest du dann das Verhältnis.

Da sollte sich viel ausser a und b rauskürzen.

---

Irgendwie sollte das so lauten:

Stelle dafür jetzt die Volumen- und die Oberflächenformel des Rotationskörpers auf.

---

Die Rotationsformel für die Rotation über b habe ich!
Aber die wenn ich über  a  Rotiere verstehe ich nicht..?

---

Steh da irgendwie total am Schlauch :/

Danke schon mal Mathecoach !!!

---

Könntest du bitte ein Bild deiner Lösung ins Kommentar geben?
Wäre echt super hab morgen bereits die Prüfung!!

---

b: Unterseite

a: Oberseite

h: Höhe

s: Seite

Volumen bei Rotation um b

V = pi·h^2·a + 1/3·pi·h^2·(b - a) = pi/3·h^2·(2·a + b)

Volumen bei Rotation um a

V = pi·h^2·b - 1/3·pi·h^2·(b - a) = pi·h^2·(a + 2·b)/3

Das Verhältnis der Volumen

pi/3·h^2·(2·a + b) / (pi·h^2·(a + 2·b)/3) = 5/6

(2·a + b)/(a + 2·b) = 5/6

Oberfläche bei Rotation um b

O = 2·pi·h·a + 2·pi·h·s = 2·pi·h·(a + s)

Oberfläche bei Rotation um a

O = 2·pi·h·b + 2·pi·h·s = 2·pi·h·(b + s)

Das Verhältnis der Oberflächen

2·pi·h·(a + s)  / (2·pi·h·(b + s)) = 29/35

(a + s)/(b + s) = 29/35

Wir erhalten also die folgenden Gleichungen

a + b + 2·s = 32

(2·a + b)/(a + 2·b) = 5/6

(a + s)/(b + s) = 29/35

Kontroll-Lösung: a = 4 ∧ b = 7 ∧ s = 10.5