Aufgabe:
Ein Künstler bereitet für eine Ausstellung im Freien eine Installation vor. Dafür hat er fünf verschieden große, dreieckige Segeltcher hergestellt.
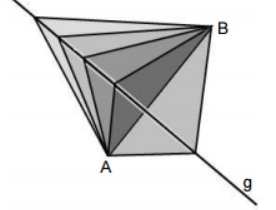
Ansicht der Installation von oben (nicht maßstabsgetreu)
In den Punkten \( A(5|3| 1) \) und \( B(-3|7| 9) \) des Geländes sollen jeweils zwei Ecken aller fünf Segeltücher befestigt werden. Die jeweils dritte Ecke der fünf Segeltücher soll in verschiedenen Punkten der Schar \( C_{k}(2+k|-3+4 k| 10-k) \) mit \( k \in \mathbb{R} \) so angebracht werden, dass die Tücher straff gespannt sind und fünf ebene Dreiecke bilden.
Um die dritte Ecke der Tücher jeweils im Punkt \( C_{k} \) zu befestigen, wird ein Seil gespannt. Dieses Seil wird durch die Gerade \( g \) beschrieben (s. Abb.). Es gilt: \( 1 \mathrm{LE}=1 \mathrm{~m} \).
a) Geben Sie eine Gleichung für \( g \), auf der alle Punkte \( C_{k} \) liegen, an. Zeigen Sie, dass die Gerade durch \( A \) und \( B \) und die Gerade \( g \) windschief sind.
b) Ein Segeltuch wird in \( A, B \) und im Punkt \( C_{0} \) befestigt. Zeigen Sie, dass dieses Segeltuch die Form eines gleichschenkligen Dreiecks hat. Bestimmen Sie die Größe der Basiswinkel.
Berechnen Sie die Fläche des Segeltuchs in \( \mathrm{m}^{2} \).
c) In der Ebene, zu der \( A \) und \( B \) symmetrisch liegen, sollen Stahlschnüre zwischen den Segeltüchern gespannt werden. An den Stahlschnüren sind farbige Strahler befestigt, um die Segeltücher abends anzuleuchten.
Geben Sie eine Gleichung der Ebene \( E \), in der die Stahlschnüre liegen, in Koordinatenform an.
Zeigen Sie, dass alle Stahlschnüre am Seil aus Aufgabe a) befestigt werden können.
d) Begründen Sie, dass alle fünf Segeltücher die Form eines gleichschenkligen Dreiecks haben.
e) Bestimmen Sie die Koordinaten des Punktes \( C_{k} \), an dem das Segeltuch mit der kleinstmöglichen Fläche befestigt werden müsste.
Ansatz/Problem:
Ich komme bei c) nicht weiter, weil ich die Sache mit der Symmetrie nicht verstehe.