Schatten die durch Sonnenstrahlen und einen Gegenstand entstehen

Question

Aufgabe:

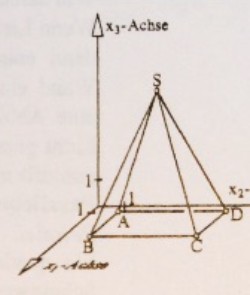
a) Berechnen und zeichnen Sie den Schatten, der entsteht, wenn die quadratische Pyramide mit der Kantenlänge 4 Koordinateneinheiten und der Höhe 5 Koordinateneinheiten von der Sonne beschienen wird und die Sonnenstrahlen die Richtung \( \vec{v} \) aus dem vorangegangenen Beispiel haben.

Parallele Lichtstrahlen fallen aus der Richtung \( \overrightarrow{\mathrm{v}}=\left(\begin{array}{c}0,5 \\ -2 \\ -1\end{array}\right) \) auf die Pyramide.

b) Berechnen und zeichnen Sie den Schatten, der am Boden und an der Wand \( \left(\mathrm{x}_{1}-\mathrm{x}_{3}\right. \)-Ebene \( ) \) entsteht.

Hinweis: Berechnen Sie zunächst den Schattenpunkt von \( \mathrm{S} \) am Boden, um die "Knickstellen" an der \( x_{1} \)-Achse zu erhalten.

Bearbeiten Sie die Fragestellung für eine Zentralprojektion mit einer Lichtquelle L(0|2|10).

Answer 1

Offenbar hat A die KOO (1/1/0) also S (3/3/5).

Gerade durch S mit Richtung v ist

x = (3/3/5) + r* (o,5 / -2 / -1 )

Diese trifft den Boden wenn  0 = 5 - r also r=5 das wäre ( 5,5/ -7 / 0)

wenn die Wand nicht da wäre.