Warum ist damit die Aussage (Fläche unter einer Parabel nach Archimedes) gezeigt? (Parabel mithilfe der Simpsonregel)

Question

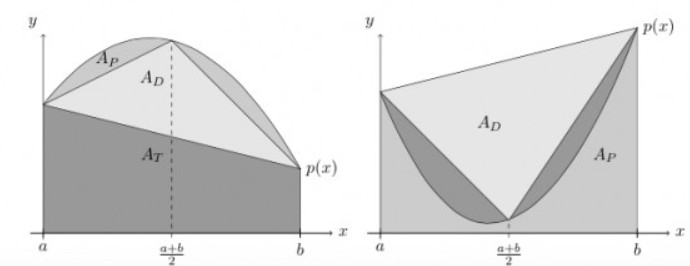
Aufgabe:

Sei $p \in \mathcal{P}_{2}$ eine Parabel mit $\left.p\right|_{[a, b]} \geq 0$ auf dem Intervall $[a, b] \subset \mathbb{R},(a<b)$.

Zeigen Sie:

$A_{P}=A_{T}+\frac{4}{3} A_{D}$

wobei

$A_{P}:=\int \limits_{a}^{b} p(x) \mathrm{d} x$

die Fläche unter der Parabel (grau), $A_{D}$ die Fläche des Dreicks mit den Eckpunkten $(a, p(a)),(b, p(b))$ und $\left(\frac{a+b}{2}, p\left(\frac{a+b}{2}\right)\right)$ (hellgrau) und $A_{T}$ die Fläche des Trapezes mit den Eckpunkten $(a, 0),(b, 0),(a, p(a))$, $(b, p(b))$ (dunkelgrau) ist, vgl. Abbildung.

Warum ist damit die Aussage aus der Vorlesung - Beispiel (1.3) 1) (Fläche unter einer Parabel nach Archimedes) - gezeigt?

Hinweis: Verwenden Sie die Simpson-Regel. Die Fläche des Dreiecks ist als negativ zu werten, falls die Parabel nach unten geöffnet ist.

Answer 1

Nimm eine allgemeine Parabel

f(x) = ax² + bx + c

Berechne dann allgemein die beiden Formeln für A_P und zeige das sich das gleiche ergibt.

Du solltest in beiden Fällen auf den Term

AP = - a·r³/3 + a·s³/3 - b·r²/2 + b·s²/2 - c·r + c·s

kommen.

* r und s sind die Integrationsgrenzen und ersetzen a und b. Das hatte ich nur gemacht, damit ich die allgemeine Parabelgleichung von den Buchstaben her nicht abändern muss. Es steht dir frei dies zu tun und die Integrationsgrenzen bei a und b zu belassen.