Aufgabe Abstandsspiel:
Nebenstehend sind die Netze zweier Würfel W1 und W2 abgebildet. W1 ist ein üblicher Laplace-Würfel, W2 ist durch Neubeschriftung aus einem solchen entstanden.
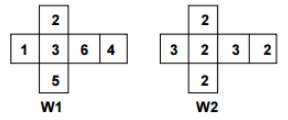
Das Abstandsspiel hat folgende Regeln:
- Einer der beiden Würfel wird zweimal geworfen.
- Einer der beiden Würfel wird zweimal geworfen.
- Es wird die Differenz der beiden Würfelergebnisse so gebildet, dass sie nicht negativ ist.
- Diese Zahl - also der Abstand der Würfelergebnisse - ist das Ergebnis des Spiels.
Beispiele:
- "2" und "6" gewürfelt, Ergebnis: 6 - 2 = 4 (der Abstand von 2 und 6);
- "2" und "2" gewürfelt, Ergebnis: 2 - 2 = 0 (der Abstand von 2 und 2).
a) Bestimmen Sie sowohl für den Würfel W1 als auch für den Würfel W2 die Wahrscheinlichkeiten der folgenden Ereignisse bei diesem Abstandsspiel:
A: Das Ergebnis beträgt 0.
B: Das Ergebnis ist ungerade. (Hinweis: null ist eine gerade Zahl.)
[Zur Kontrolle: Für den Würfel W1 gilt \( P(A)=\frac{1}{6} \), für W2 gilt \( P(A)=\frac{5}{9} \).]
Ansatz/Problem:
Hab auch schon ein Baumdiagramm gemacht mit Gerade und Ungerade, aber komme nicht auf das Lösungsergebnis.
Ich rechne immer von wegen Gerade * Gerade zum beispiel, weil bei A zum Beispiel ist ja gefragt, wie man zu 0 kommt. Das ist nach meiner Meinung jedes Ergebnis mit sich selbst. Also ungerade * ungerade und Gerade * Gerade. Das muss doch dann 0,5 * 0,5 sein oder nicht und somit 0,25 oder nicht? Wo denke ich denn da falsch?
Und bei B wollte ich eigentlich so ähnlich vorgehen... nur das Endergebnis dann halt mit der aufgabe von A multiplizieren.