Der Aufgabensteller scheint nicht sehr intelligent zu sein, denn ohne Randbedingungen gibt es unendlich viele Lösungen (Algorithmen für Zahlenfolgen)!
Neben den beiden hier genannten noch 3 weitere per Iterationsrechner:
http://www.gerdlamprecht.de/Roemisch_JAVA.htm##@N@B0]=1;a=0;i=1;@N@Bi]=(i%252%3E0)?@Bi-1]*(a=a+1):@Bi-1]+a;@Ci]=floor(@Pi+1,2)/4);aD[i]=(i-1)*2+floor(exp(1-i));@Ni%3E17@N0@N0@N#
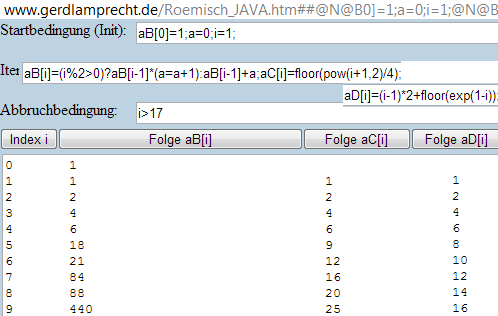
Hinweise: pow(i+1,2) = (i+1)² und floor(x) = Abrunden
exp(x) = e^x
(und ich kenne noch über 300 weitere Funktionen :-)
Die 2. von Mathecoach lautet exakt: aD[i]=Prime(i)-1;
und ergibt: 1, 2, 4, 6, 10, 12, 16, 18, 22, 28, 30, 36, 40, 42, 46, 52, 58,...
und seine 1. etwas einfacher: (12-(-7+x)*(-2+x)*x)/6 ergibt 1, 2, 4, 6, 7, 6, 2, -6,...
Allein in Pi an den Nachkommastellen-Positionen: 2287, 37848, 41957, 51658, ...
kommt diese Zahlenfolge vor -> und das unendliche Male!!
oder
floor((goldenratio)^n) ergibt 1, 2, 4, 6, 11, 17, 29, 46, 76, 122, 199...
oder aB[i]=floor((5*i-2)/3); ergibt 1, 2, 4, 6, 7, 9, 11, 12, 14, 16, 17, 19, 21,...