Es gibt zwei Möglichkeiten einen Winkel anzugeben:
1) Über die Einteilung des Vollkreises in 360 gleiche Teile --> Gradmaß
2) Über die Länge des Kreisbogens des Einheitskreises --> Bogenmaß
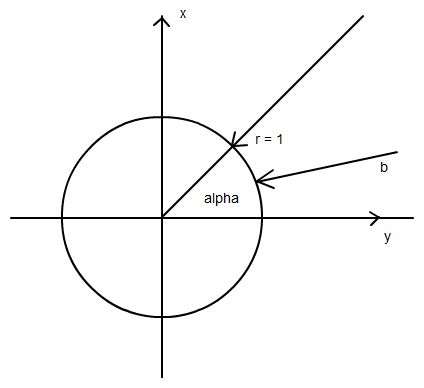
Wenn Du den Winkel im Gradmaß angibst, dann gibst Du alpha an.
Wenn Du den Winkel im Bogenmaß angibst, dann schreibst Du b. b ist die Länge des Bogens des Einheitskreises zwischen y-Achse und dem Schenkel des Winkels.
Der Umfang des Einheits kreises ist U = 2*r*pi = 2*pi da r = 1.
Der Zusammenhang zwischen Gradmaß und Bogenmaß ist:
Umrechnung von Grad in Radiant (Einheit des Bogenmaßes):
b = alpha/180° * pi
Umrechnung von Radiant in Grad:
alpha = b/pi * 180°
Beim Taschenrechner gibt es drei Auswahlmöglichkeiten:
Deg, Gra, Rad
Deg = Degree = Grad
Rad = Radian = Radiant
Gra = ? = Neugrad - beruht auf der Einteilung des Vollkreises in 400 gleiche Teile