Ermittle die Funktionsgleichung für diesen schrägen Wasserstrahl. Welcher der Wasserstrahlen erreicht eine größere Höhe?

Question

Aufgabe Wasserspeier:

Der Wasserstrahl eines Wasserspeiers verläuft in Form der unten gezeichneten Parabel. Die Wasseraustrittsdüse befindet sich direkt auf der Wasseroberfläche.

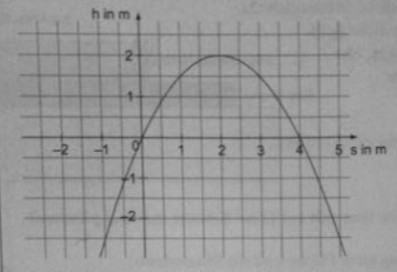
a) Gib die maximale Höhe des Wasserstrahls an.

b) Ist es sinnvoll einen solchen Wasserspeier in einen Gartenteich mit einem Durchmesser von \( 3 \mathrm{~m} \) einzusetzen?

c) Welche quadratische Funktion beschreibt den Wasserstrahl dieses Wasserspeiers, wenn gilt \( a>0, b>0 \) und \( c>0 \)?

I \( y=a \cdot x^{2} \)
II \( y=-a \cdot x^{2} \)
III \( y=-a \cdot x^{2}+b \cdot x+c \)
IV \( y=-a-x^{2}+b \cdot x \)

Begründe, warum die anderen quadratischen Funktionen den Wasserstrahl nicht beschreiben.

d) Ermittle die Funktionsgleichung für diesen schrägen Wasserstrahl.

e) Für zwei andere Wasserstrahlen gelten folgende Funktionsgleichungen:

Wasserstrahl 2: \( y=-4 \cdot x^{2}+4 \cdot x \)

Wasserstrahl 3: \( y=-1,5 \cdot(x-1)^{2}+1,50 \)

Welcher der beiden Wasserstrahlen erreicht eine größere Höhe? Begründe.

Answer 1

max Höhe 2m
nein, der sprüht 4m weit
c) I müsste der Hochpunkt auf der y-Achse liegen und Parabel wäre nach oben geöffnet

II   ist zwar nach unten geöffnet aber immer noch Hochpunkt auf y-Achse

III für c>o ginge es nicht durch den Nullpunkt

IV das passt  

mit y = -ax^2 + bx  und durch (2/2) und ( 4/0) hat man
2 = -a*4 + b*2      und  0  = -a * 16 + 4b
2 + 4a = 2b
4 + 8a = 4b                    0 = -16a + 4 + 8a
                                        8a = 4
                                          a = 1/2 
8 = 4b
2 = b     also    y = - 0,5 x^2   +   2 x

Scheitelpunkte bestimmen bei 2:    S(0,5  /  1 )
                                                     bei 3     S ( 1 /  1,5 )
also bei 3 am höchsten.

Comments

 Ich habe für die Funktionsgleichung das hier raus : y = -1 (x -2) +2 

ist das etwa falsch ? 

---

Ja , das ist falsch, da ja schonmal das Quadrat fehlt.

Du hast eine Gerade genommen, das ist aber eine Parabel.

Answer 2

d)

Scheitelpunktform

a = Δy / (Δx)² = -2 / 2^2 = -1/2

f(x) = -1/2 * (x - 2)^2 + 2

e)

y = -4x^2 + 4x 

y = -4(x^2 - x + 0.25 - 0.25)

y = -4(x^2 - x + 0.25) + 1

y = -4(x - 0.5)^2 + 1

Dieser erreicht eine Höhe von 1 m. Der zweite eine Höhe von 1.5 m. Damit ist der zweite höher.

Comments

ich verstehe nicht ganz die rechen bei e) 

könntest du mir das vielleicht erklären

---

Das ist die Umformung in die Scheitelpunktform

Schau eventuell mal unter https://www.mathelounge.de/57/wie-kann-die-normalform-eine-scheitelpunktform-umwandeln