Mathematikaufgabe: Muster in geometrischen Figuren
Untersuchen Sie das vorliegende Parkett:
a) Welche der folgenden Eigenschaften hat das abgebildetet Parkett? Einfach, regulär, platonisch, archimedisch, periodisch?
Begründen Sie Ihre Entscheidungen stichwortartig! (wenn ja oder nein, warum?)
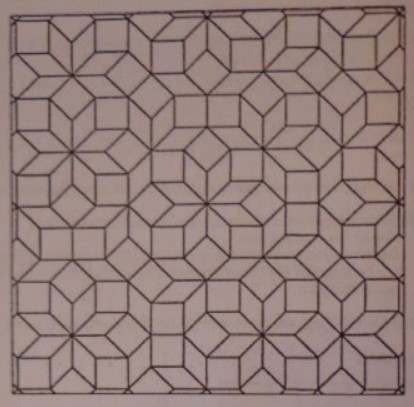
b) Zeichnen Sie alle im Parkett vorkommenden Polygone und notieren Sie die Namen dieser Polygone?
c) Berechnen Sie alle in den Polygonen vorkommenden Innenwinkel. Dokumentieren Sie dabei Ihre Überlegungen zum Berechnungsweg.
d) Zeichnen Sie die Symmetrieachsen und Symmetriepunkte der Polygone ein.
e) Sind die einzelnen Polynome parkettierbar? Begründen Sie die (Nicht)Parkettierbarkeit!
f) Zeichnen Sie im Falle der Parkettierbarkeit wenn möglich jeweils zwei verschiedene Parkette der Polygone.
g) Notieren Sie die Eigenschaften der von Ihnen gezeichneten Parkette.
Reflexion / Sachanalyse: Welches Thema, welcher Sachverhalt oder welches Problem wird behandelt? (mathematische Grundvoraussetzungen, mathematische Tâtigkeiten, Zusammenhänge zu andern Themen, mathematische Kernidee, ...)